Напишу полный ход своих рассуждений, а то такая каша в голове, не могу разобраться.
Есть гиперболический синус:
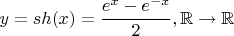
Попробую найти для него обратную функцию:
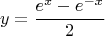
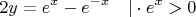
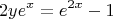
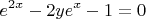
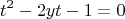
Получили квадратное уравнение с параметром

, относительно переменной

.
Дискриминант
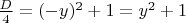
получается строго положительным, значит уравнение (которое относительно

) имеет два корня независимо от

. Найдем корни:
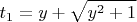
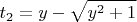
Легко показать, что

всегда положительный, а

всегда отрицательный, значит

нам не подходит (у нас же

), значит подходит только

. В общем,
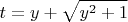
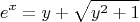
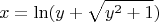
Мы смогли выразить

независимо от

, причем однозначным образом. Это значит, что существует функция, обратная к нашему гиперболическому синусу - ареасинус:
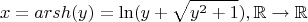
Я проверил по википедии, формула правильная, пока у меня сомнений нету.
Дальше я решил продифференцировать этот ареасинус по

. Но эту прямую формулу я пока дифференцировать не буду, а сделаю вот как (через производную обратной функции):
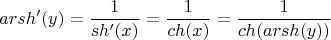
Дальше я пользуюсь формулой:
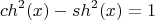
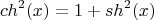
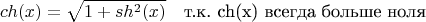
То есть,
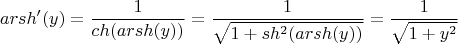
Пока все в порядке, формула вроде правильная получается.
Дальше я беру неопределенный интеграл от полученной дроби на связном множестве

:
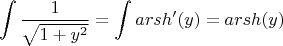
(Оффтоп)
Я не пишу в интегралах dx, вообще не понимаю зачем это надо. Интеграл - просто оператор, берущий функцию на связном множестве и все. И +C тоже не пишу, просто под равенством понимается более слабое отношение эквивалентности с точностью до прибавления константы.
Но ведь тогда получается, что если я смогу взять интеграл
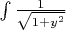
элементарными методами (обычной тригонометрией, без гиперболических функций), я же должен по итогу получить то же самое выражение, которое я получил для ареасинуса выше:
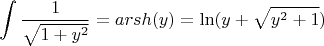
Так ведь?
А у меня вообще какая-то ерунда получается, даже близко не то.