Очевидность корней кубического уравнения

[sydorov]

$\[ \lambda^3 - 18\lambda^2 + 64\lambda - 64 = 0 \]$

В пособии, которым пользуюсь, сказано "Очевидным корнем этого уравнения является $\[\lambda_1 = 2\]$".
Подскажите, пожалуйста, лайфхак как это "разглядеть". Кроме проверки целочисленных делителей свободного члена (теорема Виета), чтобы найти один из корней, ничего не "разглядывается".

[Mikhail_K]

sydorov в сообщении #1700710 писал(а):

Кроме проверки целочисленных делителей свободного члена (теорема Виета), чтобы найти один из корней, ничего не "разглядывается".

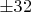
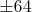
Только так и разглядеть. Ещё может быть имелось в виду, что приниматься за скрупулёзный перебор всех делителей вплоть до $\pm 32$ и $\pm 64$ выглядит чем-то слишком долгим, но уж $\pm 1$ и $\pm 2$ нетрудно подставить - авось повезёт.

-- 04.09.2025, 18:14 --

sydorov в сообщении #1700710 писал(а):

теорема Виета

Кстати, а при чём тут теорема Виета? Из неё следует только то, что если все корни целые, то они делители свободного члена.

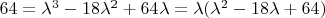
Но даже если не все корни целые, а хотя бы один корень целый, то он обязательно будет среди делителей. Это следует уже не из теоремы Виета, а из того, что если $\lambda$ - целый корень, то $64=\lambda^3-18\lambda^2+64\lambda=\lambda(\lambda^2-18\lambda+64)$ делится на $\lambda$.

[sydorov]

Mikhail_K, спасибо большое, что прояснили. До этого полистал пару простых книг на эту тему, а там только формула Кардано.

[nnosipov]

Mikhail_K в сообщении #1700715 писал(а):

Из неё следует только то, что если все корни целые, то они делители свободного члена.

Из нее следует утверждение в самом общем случае, но доказательство перестает быть школьным. Видимо, школьники (да и студенты тоже) в этом месте ссылаются на теорему Виета из-за наглядности, хотя доказывать утверждение о делимости на ее основе себе дороже будет.

[wrest]

sydorov в сообщении #1700710 писал(а):

В пособии, которым пользуюсь, сказано "Очевидным корнем этого уравнения является $\[\lambda_1 = 2\]$".
Подскажите, пожалуйста, лайфхак как это "разглядеть".

Перебором того что можно "увидеть" в уме.
Ноль и обе единицы выпадают сразу.
Так что двойка это первое что надо проверить подстановкой "в уме".
Для облегчения подсчета в уме приводим подобные: $x^3-18x^2+64x-64=x^2(x-18)+64(x-1)$ или иначе $64(x-1)=x^2(18-x)$ откуда очевидность двойки прям видна

[sydorov]

wrest, согласен с вами

[Утундрий]

Издевательская версия задачи: взять свободный член в виде $2^{100}$, а единственный целый корень положить равным $2^{53}$.

[sydorov]

Утундрий,

(Оффтоп)

Проверяя вручную, можно постичь дзен

[maxmatem]

А чем схема Горнера не угодила ?

[b4b5]

Теорема Безу подходит.