Матфизика: сопротивление трапецевидной пластинки

[reterty]

Рассмотрим проводящую пластинку, сделанную из материала с удельной электропроводностью $\sigma$ и имеющую всюду постоянную толщину. Пусть пластинка имеет вид равнобокой трапеции, к основаниям-граням которой приложено постоянное напряжение $U$. Задача состоит в отыскании сопротивления такой пластинки. Вследствие наличия эффекта изгиба линий электрического поля, задача сводится к решению двумерного уравнения Лапласа $\Delta \varphi=0$. 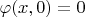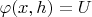Если направить ось $y$ от одного основания пластины к другому, а ось $x$ перпендикулярно, то будем иметь дело со смешанными граничными условиями: $\varphi(x, 0)=0$; $\varphi(x, h)=U$, где $h$-высота трапеции. Имеется также третье условие, состоящее в том, что нормальная к боковым граням производная потенциала должна обращаться в нуль. Тогда ток через произвольное сечение пластинки, параллельное основаниям найдется так: $$I=\sigma \int_S \dfrac{\partial \varphi}{\partial y} {\rm d}S$.

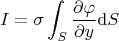
Сформулирую вопрос: можно ли в рамках такой задачи, с изгибом электрического поля, априорно утверждать что сопротивление пластинки $R=U/I$ и в таком случае будет оставаться постоянным, независящим от напряжения $U$ как и случае проводника с постоянным поперечным сечением по длине ? Возможно, здесь для доказательства можно использовать условие масштабируемости, возникающее в силу линейности уравнения Лапласа а также теоремы о единственности его решения?

[Theoristos]

reterty в сообщении #1699634 писал(а):

можно ли в рамках такой задачи, с изгибом электрического поля, априорно утверждать что сопротивление пластинки $R=U/I$ и в таком случае будет оставаться постоянным

А это как раз "априорно", "по определению".
Чисто постулативная закономная связь, только не $U$ и $I$, а $\vec{E}$, $\vec{J}$.
В более других случаях может быть и иначе.

ps: при решении не забыть, что заряды создающие поле будут и на боковых сторонах пластинки.

[Alex Krylov]

См. Van Bladel J. - Electromagnetic Fields, стр.149-150 и на стр. 149 обратите внимание на утверждение:

Цитата:

The potential is clearly proportional to $V$, hence it can be written as $V\varphi_1$, where $\varphi_1$ corresponds with the condition $V = 1$

или в переводе

Цитата:

Потенциал $\varphi$ очевидно пропорционален $V$, следовательно он может быть представлен в виде $V\varphi_1$, где $\varphi_1$ - потенциал для случая $V = 1$