Так как
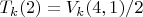
- ополовиненная последовательность Люка с дискриминантом

,
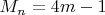
и символ Якоби
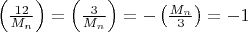
, то

будет
псеводопростым Люка, если
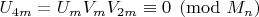
. Вы по сути доказали, что для простого

,
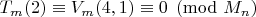
, что влечет как условие теста Люка, так и
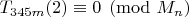
. Однако непонятно, чем предложенный тест лучше теста Люка, у которого кроме того есть "сильные" варианты, а также чем обусловлен множитель

перед

(с тем же успехом можно взять любое другое нечётное число).
Известно, что тест Люка допускает наличие псевдопростых, однако среди таких разреженных (ввиду экспоненциального роста) чисел как

их может не существовать, как, впрочем, и у предложенного теста.