Теорема Ферма и гипотеза об эффективно вычислимом потолке1. Теорема Ферма и генерация систем Виета.Пусть для некоторых целых (натуральных) чисел a, b, c выполнено равенство
\bigskip
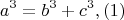
тогда k- также целое (натуральное)

и выполняются равенства
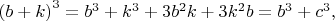
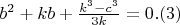
Относительно неизвестной b- уравнение (1) кубическое, и по формулам Виета получаем
систему уравнений
\bigskip
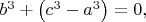
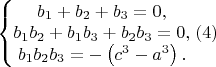
В свою очередь, уравнение (3) относительно неизвестной b уже квадратное,
следовательно выполняется система уравнений:
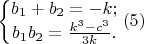
Тогда из первых уравнений систем получаем
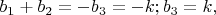
из вторых уравнений систем получаем
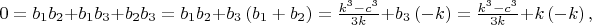

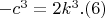
Однако, уравнение (6) неразрешимо ни в натуральных числах, ни в целых вещественных числах. Обобщение на случай произвольного значения n очевидно и можно провести многими способами, есть 2n-1 уравнений, а неизвестных только n+3
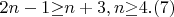
\bigskip
Постников. стр.9. {\textquotedbl}Элементарное же доказательство теоремы Ферма ... ЗАКРОЕТ ПРОБЛЕМУ, но большого значения
для математики иметь заведомо не будет{\textquotedbl}. Почти.
Замечание 1. Что-то похожее получается в попытке доказательства невозможности существования нечётных совершенных чисел: если s- количество различных простых сомножителей совершенного числа N, то чётным оно является тогда и только тогда, когда s=2. При s>2 количество неизвестных равно 2s (число показателей степеней и оснований), а число возможных уравнений как минимум 4s+1. Проблема в том, что они не являются алгебраическими и методы их решения неизвестны. Возможно необходимости в поиске новых методов и нет, поскольку, с другой стороны, при заданном числовом значении s поиск нечётных совершенных чисел N всегда можно свести к конечному перебору. Таких чисел при s≤103 (как минимум, в Википедии данные устарели) нет, нижняя граница нечетного N растет как

Надо лишь найти некоторую эффективную границу s, выше которой, по сути, идет повтор математических структур.
Также проблема нечётных совершенных чисел напрямую связана с гипотезой Римана в форме критерия Робина через вычисление функции делителей σ(N). Здесь ситуация проще, только чистая алгебра, как минимум, удалось избавится от функции делителей σ(N) и упростить критерий Робина.
\bigskip
\textit{Замечание 2. }Заметим, что из первого и второго уравнений системы (4) следует
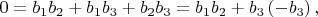
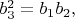
поэтому система (4) неразрешима в целых попарно взаимно простых числах
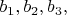
\ поскольку
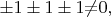
значит предположение о существовании \textbf{комплексных} чисел в данной системе \textbf{обязательно, }даже если они не
используются напрямую. В этом смысле доказательство неэлементарно. В рамках \textit{только вещественных} чисел системы
Виета вырождаются и смысла не имеют.
\bigskip
Конкретно для \textit{кубического} уравнения, важно, что корнями алгебраического уравнения могут быть только
комплексно-сопряженные корни (всегда в чётном количестве) либо вещественные. Тогда система (5) разрешима либо только в
целых числах

\ либо только комплексных числах

. Значит, системы (4) и (5) неразрешимы в целых
числах одновременно, это противоречие, поскольку при подстановке
\bigskip
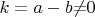
они эквивалентны. Очевидно, что данная подстановка может быть полезна для всех диофантовых уравнений с любым количеством
переменных \foreignlanguage{english}{\textit{s}}. Число порождаемых подобным образом систем Виета равно \ \
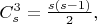
если произошло \textit{понижение} степени, то не все они будут тривиальными. Например, подобным образом можно доказать неразрешимость диофантового уравнения
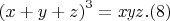
\bigskip
Аналогично для уравнения
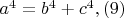
получаем сопряжённое уравнение
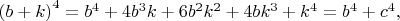
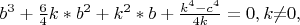
и две системы уравнений по формулам Виета:
\bigskip
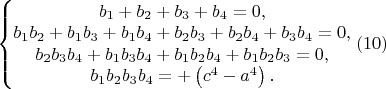
\bigskip
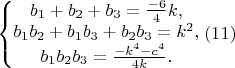
Тогда из первых уравнений систем получаем
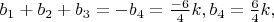
из вторых уравнений систем получаем
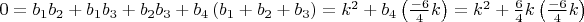
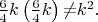
Таким образом, поскольку
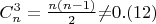
системы несовместны при {\textit{n}}
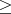
4, если
{\textit{k}}\textit{

0}. \
Заметим, что все четные совершенные числа также имеют вид (12), это к гипотезе о \textbf{повторе математических
структур. }
Также из предпоследних уравнений систем можно получить
\bigskip
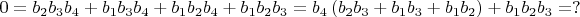

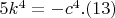
В общем случае получаем неразрешимость в \textit{целых} числах уравнения
\bigskip
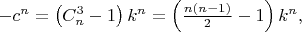
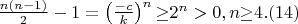
\bigskip
\bigskip
2. Гипотеза об эффективном потолке, бесконечный спуск и дерево вариантов.
\bigskip
1.Пусть диофантово уравнение содержит \textit{конечное}\textbf{ }число переменных и \textit{конечное} число операций
(функций) сложения, умножения, возведения в степень и только их.
2. Нет других операций и арифметических функций наподобие функции делителей
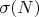
, функций Мёбиуса
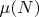
,
функций

пол

и

потолок

либо от
них можно каким-либо образом избавится.
\ \ \ Операция умножения суть многократное сложение, в свою очередь операция возведения в степень суть многократное
умножение, поэтому конечные диофантовы уравнения

это математическая структура из
\textit{комбинаций} только одной операции сложения, сами числа

это сумма единиц.
Имеем\foreignlanguage{english}{, }например\foreignlanguage{english}{, }диофантово уравнение
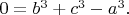
Ввиду малости всех переменных и коэффициентов интуитивно представляется очевидным, что при отсутствии натуральных
решений в достаточно большом диапазоне, например при \
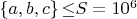
\bigskip
решений не будет в принципе! При больших значениях переменных идет \textbf{повторение математических структур }(сам этот
термин неопределяем, он зависит от аксиоматики). \textbf{\ }Но как это доказать?
Этот же диапазон должен задавать все серии нетривиальных решений, если таковые найдутся.
Сформулируем две рабочие \textit{гипотезы}.
\begin{enumerate}[series=listWWNumiv,label=\arabic*.,ref=\arabic*]
\item Для каждой переменной в конечном диофантовом уравнении существует эффективно вычислимый потолок значений, задающий
все натуральные решения данного уравнения.
\end{enumerate}
Тогда задачу поиска решений можно принципиально свести к \textit{полному перебору}. \
В частности, если для такого уравнения в достаточно большом диапазоне
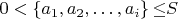
не найдено ни одного целого решения, то из нет вообще.
\begin{enumerate}[resume*=listWWNumiv]
\item В \textit{некоторых} диофантовых уравнениях число \textit{математических структур }конечно. Это обобщение, какими
свойствами должны обладать эти уравнения?
\end{enumerate}
\bigskip
Есть принципиальное сходство с \foreignlanguage{english}{\textit{abc}}{}-гипотезой, но она оперирует с
\textit{элементами} множеств (конкретно числами), а гипотеза (1) об эффективном потолке конечных диофантовых уравнений
работает с самими \textit{операциями, }и её вроде бы легче доказать. \
\bigskip
Заменив сложение умножением, умножение возведением в степень, возведение в степень
возведением в двойную степень можем получить максимальное число сочетаний операции \foreignlanguage{english}{\textit{S}}
“сложение/вычитание” в уравнении.
Пусть число переменных-оснований показателей степеней в уравнении \foreignlanguage{english}{\textit{i}},
произведение коэффициентов при них равно \foreignlanguage{english}{A},
число переменных-показателей степеней равно \foreignlanguage{english}{\textit{j}},
и произведение коэффициентов при них равно \foreignlanguage{english}{B},
тогда
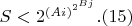
Для уравнения (1) получим
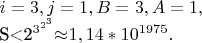
\bigskip
Аргументам

\ добавим \textit{всевозможные} натуральные приращения
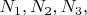
\ такие, что
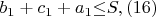
получим формы вида
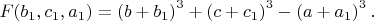
По условию
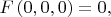
\ тогда для \textit{всего дерева} вариантов для меньшей ветки \textbf{должно
выполняться условие }(это надо проверить)
\bigskip
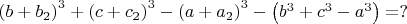
![$=K\left[\left(b+b_1\right)^3+\left(c+c_1\right)^3-\left(a+a_1\right)^3-\left(b^3+c^3-a^3\right)\right],(17)$ $=K\left[\left(b+b_1\right)^3+\left(c+c_1\right)^3-\left(a+a_1\right)^3-\left(b^3+c^3-a^3\right)\right],(17)$](https://dxdy-01.korotkov.co.uk/f/4/d/7/4d723f9ea00c9e357f7bfbe599d2837082.png)
\foreignlanguage{english}{\textit{K}}{}- целое либо полином.
Из набора
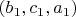
\ \textit{хотя бы одно} из чисел должно быть меньше соответствующего числа из
набора\textit{ }
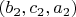
\textit{.\ \ }
Если \foreignlanguage{english}{K
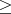
2, }и выполнено
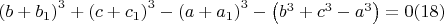
то это набор уникальных корней.
Подобный перебор

это бесконечный спуск брутфорсом. Начиная с некоторой глубины (корней), каждая
ветвь будет \textit{линейной комбинацией} меньших ветвей. Глубина дерева, скорее всего, будет\foreignlanguage{english}{
} порядка
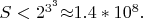
Этим элементарное доказательство отличается от неэлементарного: количество вариантов, которых надо проверить растет по экспоненте, для общего случая, вероятно, порядка 10^9.
Для случая \foreignlanguage{english}{\textit{n}}=2 уникальный корень только один (3,4,5) (за исключением перестановки
(4,3,5)), остальные получаются умножением на матрицы
![$A=\left[\begin{matrix}\begin{matrix}1&\begin{matrix}-2&2\end{matrix}\\2&\begin{matrix}-1&2\end{matrix}\end{matrix}\\\begin{matrix}2&-2&3\end{matrix}\end{matrix}\right],B=\left[\begin{matrix}\begin{matrix}1&\begin{matrix}2&2\end{matrix}\\2&\begin{matrix}1&2\end{matrix}\end{matrix}\\\begin{matrix}2&2&3\end{matrix}\end{matrix}\right],C=\left[\begin{matrix}\begin{matrix}-1&\begin{matrix}2&2\end{matrix}\\-2&\begin{matrix}1&2\end{matrix}\end{matrix}\\\begin{matrix}-2&2&3\end{matrix}\end{matrix}\right].$ $A=\left[\begin{matrix}\begin{matrix}1&\begin{matrix}-2&2\end{matrix}\\2&\begin{matrix}-1&2\end{matrix}\end{matrix}\\\begin{matrix}2&-2&3\end{matrix}\end{matrix}\right],B=\left[\begin{matrix}\begin{matrix}1&\begin{matrix}2&2\end{matrix}\\2&\begin{matrix}1&2\end{matrix}\end{matrix}\\\begin{matrix}2&2&3\end{matrix}\end{matrix}\right],C=\left[\begin{matrix}\begin{matrix}-1&\begin{matrix}2&2\end{matrix}\\-2&\begin{matrix}1&2\end{matrix}\end{matrix}\\\begin{matrix}-2&2&3\end{matrix}\end{matrix}\right].$](https://dxdy-01.korotkov.co.uk/f/8/4/d/84d0f4124a46e9775d59a9767b9dbe7a82.png)
Необходимо проверить выполняется ли условие (17) для случая n=3.