Задачи из учебника Лузина

[Combat Zone]

Without Name в сообщении #1698352 писал(а):

В этом есть какой-то смысл? Может это какой-нибудь канонический вид уравнения параболы из аналитической геометрии?

Да, но для ваших целей этот смысл без разницы. Могли и оставить скобки. Могли и раскрыть. Дело хозяйское.
Конечно, чтобы было лучше видно "почти канонический вид". С точностью до сдвига и симметрии.

[Without Name]

Задача 6.

Под каким углом линия $y=x$ пересекает кривую $x^2 + xy + y^2 = 12$?

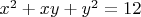
Решение:

Найдем точки пересечения прямой с кривой. Для этого подставим $y=x$ в уравнение эллипса и получим $3x^2 = 12, x = \pm 2$.

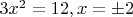
Найдем производную $y=x$, она равна 1, угол наклона этой прямой равен 45 градусам.

Найдем производную $x^2 + xy + y^2 = 12$:
$2x + xy' + y + 2yy' = 0$
$(x + 2y)y'=-2x - y$
$y'=\frac{-2x-y}{x+2y}$

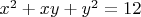
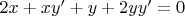
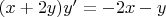
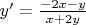
Найдем координату $y$ точек пересечения. Для этого подставим $x=\pm 2$ в уравнение эллипса. Получим два совпадающих уравнения:
$y^2-2y-8 = 0$
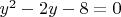
Решим его по теореме Виета, получим: $y_1=-2, y_2=4$

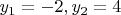
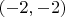
Вот тут у меня проблема. Нейросетка и Maple говорят, что точки пересечения $(2,2)$ и $(-2, -2)$. Где я ошибся?

Как мне решать задачу дальше после нахождения точек пересечения? Подставить эти точки в выражение производной и найти наклон касательных в этих точках? А как найти угол между касательными и прямой $y=x$?

-- 15.08.2025, 22:56 --



-- 15.08.2025, 23:08 --

Ой, я ошибся при составлении квадратных уравнений. При подстановке $x=\pm 2$ получится два уравнения:
$y^2 + 2y - 8 =0, y_1 = 2, y_2 = -4$
$y^2 - 2y - 8 = 0, y_1 = -2, y_2 = 4$

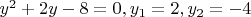
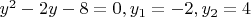
Но это все равно неправильно.

[Combat Zone]

Нет, это правильно. lel0lel правильно говорил, что это ружье рано или поздно выстрелит, вот оно и выстрелило.
Посмотрите на свою картинку. При $x=2$ в каких местах нужно искать соотв. ему $y$? Сколько их? Вот их вы и нашли.

[lel0lel]

Without Name в сообщении #1698390 писал(а):

Где я ошибся?

В уравнение прямой нужно подставлять.
Такие они -- эти уравнения эллипсов, подставляешь бывало в них два значения $x$, а они как выдадут аж четыре подходящих $y$.

[Without Name]

Понятно. Тогда подставим точки $(2, 2)$ и $(-2, -2)$ в выражение производной и получим угловой коэффициент касательной -1. Нейросетка подсказала мне формулу для вычисления угла между прямыми по их угловым коэффициентам, это $tan \alpha = \left\lvert \frac{k_1 - k_2}{1+ k_1 k_2} \right\rvert$. Применим эту формулу:

$tan \alpha = \left\lvert\frac{1+1}{1- 1\cdot 1}\right\rvert =\frac{2}{0}$. Получили неопределенность, которой соответствует бесконечное значение тангенса. Это значит, что угол между прямыми 90 градусов.

[Combat Zone]

Только что у вас задача была. Не впрок пошла, видать?

[Without Name]

Ой, да, верно. Можно перемножить угловые коэффициенты и получить -1, это значит, что прямые ортогональны.