barnashka, есть интересная книжка:
А. П. Доморяд. Математические игры и развлечения. Государственное издательство физико-математической литературы, Москва, 1961.
На странице 54 (это § 8) описывается простой способ вычисления логарифмов, используя таблицу кубов. Можно попробовать применить этот способ к вычислению
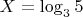
.
Пусть
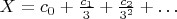
, где

— это

,

или

. Тогда
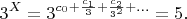
Так как
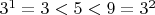
, то

и
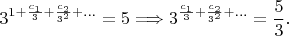
Возводя обе части в куб, получим
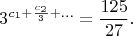
Далее удобнее перейти к приближённым десятичным числам:
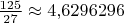
. С этого места нужно использовать нижнюю и верхнюю границы. Нижнюю границу округляем всегда вниз, верхнюю — всегда вверх. Оставляя, например,

значащие цифры, получим
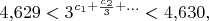
откуда

и
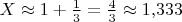
. Это совпадает с тем, что у Вас получилось.
Идём дальше. Снова делим на

и возводим в куб:
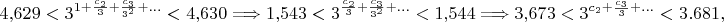
откуда

и
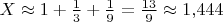
.
Повторяем те же вычисления:
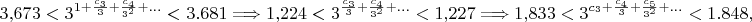
откуда
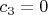
(значение
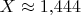
не меняется).
Возводя в куб, получаем далее
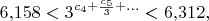
откуда
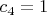
и
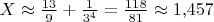
.
Следующий шаг:
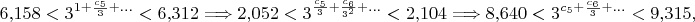
откуда получаем разные значения

для нижней и верхней границ:
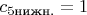
и
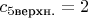
. Поэтому мы можем написать
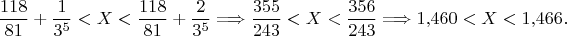
Если нужно вычислить логарифм точнее, нужно сохранять больше значащих цифр.
P.S. Я никогда не встречал обозначения "одз(1;2)". Это что означает? Когда я был школьником, аббревиатура ОДЗ или О.Д.З. (область допустимых значений) обозначала то, что сейчас называется "область определения" (функции, уравнения или неравенства).