Несуществующие существующие

[Booker48]

Большая просьба привести примеры таковых.)))
Имеются в виду математические объекты, заведомо существующие (например, доказана теорема существования), но не обнаруженные по какой-то причине. Желательно, доступные для понимания старшеклассником.
Мне приходят в голову только примеры типа алгоритм пересчёта алгебраических чисел: получить алгебраическое число по его номеру и наоборот. И то, честно говоря, не уверен, что кто-нибудь уже не построил такой.

[dsge]

Неизмеримое множество.

[dgwuqtj]

Вполне упорядочивание $\mathbb R$, иррациональное число среди $\zeta(5), \zeta(7), \zeta(9), \zeta(11)$.

Из другой области — числа вроде "самое маленькое натуральное число, не представимое в виде арифметического выражения длины меньше 40". Они очевидно существуют и даже небольшие (т.е. можно записать на бумаге), но вот явно посчитать сложно.

[Booker48]

dsge в сообщении #1695586 писал(а):

Неизмеримое множество.

Увы, безнадёжно слаб я в топологии и около неё. Но в "Контрпримерах в анализе" Гелбаум и Олмстед такое множество вроде строят, или что-то другое имеется в виду?

dgwuqtj в сообщении #1695588 писал(а):

...иррациональное число среди $\zeta(5), \zeta(7), \zeta(9), \zeta(11)$

Насколько я понимаю, иррациональность этих значений не доказана? Если да, то это не совсем то, кмк. Наверное, подошёл бы обратный пример, когда доказано, что некое число - рационально, но не найдены $p$ и $q$.

dgwuqtj в сообщении #1695588 писал(а):

Из другой области — числа вроде "самое маленькое натуральное число, не представимое в виде арифметического выражения длины меньше 40". Они очевидно существуют и даже небольшие (т.е. можно записать на бумаге), но вот явно посчитать сложно.

Тогда ещё подошло бы что-то вроде "арифметическая прогрессия длиной 100 из простых чисел". По теореме Грина-Тао длина может быть любой, но максимальная известная такая АП состоит из 29 чисел.

[mihaild]

Booker48 в сообщении #1695592 писал(а):

Но в "Контрпримерах в анализе" Гелбаум и Олмстед такое множество вроде строят, или что-то другое имеется в виду?

Да, там стандартная конструкция.

Booker48 в сообщении #1695592 писал(а):

Насколько я понимаю, иррациональность этих значений не доказана?

Известно, что хотя бы одно из них иррационально. Но какое конкретно (а так же одно среди них иррациональное, два, три, или все четыре) - неизвестно.

[EUgeneUS]

Рассмотрим цепочки последовательных натуральных чисел, имеющих одинаковое количество делителей $k$ (рассматривались в теме "Пендадекатлон мечты").
Для любого фиксированного $k$
1. такие цепочки ограничены.
То есть существует $n(k)$ - максимальная длина цепочки последовательных натуральных чисел, имеющих ровно $k$ делителей.
2. Границу сверху можно молучить теретически (с некоторыми $k$ даже с этим имеются сложностм).
3. А вот существование цепочки с максимальной длиной гарантируется гипотезой Диксона, то есть не доказано.
4. Для некоторых $k$ такие цепочки найдены, а значит $n(k)$ найдено и доказано его значение.
5. Но далеко не для всех

[dgwuqtj]

Booker48 в сообщении #1695592 писал(а):

Но в "Контрпримерах в анализе" Гелбаум и Олмстед такое множество вроде строят, или что-то другое имеется в виду?

Оно явно не предъявляется. Стандартная конструкция основана на том, что есть некое множество $X$ вещественных чисел, элементы которого имеют иррациональные разности, а любое вещественное число отличает от элемента $X$ (единственного) на рациональное число. Явно такое множество построить нельзя.

[dsge]

Booker48 в сообщении #1695592 писал(а):

Но в "Контрпримерах в анализе" Гелбаум и Олмстед такое множество вроде строят, или что-то другое имеется в виду?

Имелся в виду пример из Колмогорова и Фомина. dgwuqtj описал конструкцию. В Гелбаум и Олмстеде некие манипуляции с Канторовым множеством, чтобы построить то что они определяют как "множество без площади", кажется, что это их определение отличается от определения неизмеримого множества в КФ.

Booker48 в сообщении #1695583 писал(а):

заведомо существующие (например, доказана теорема существования), но не обнаруженные по какой-то причине.

Теоремы о неподвижных точках, типа Брауэра или Какутани. Объекты точно существуют, будь-то решения нелинейных УЧП или равновесия Нэша. Но как найти и сколько их?

[mihaild]

dsge в сообщении #1695617 писал(а):

В Гелбаум и Олмстеде некие манипуляции с Канторовым множеством, чтобы построить то что они определяют как "множество без площади", кажется, что это их определение отличается от определения неизмеримого множества в КФ

В 11 примере 8 главы они строят стандартный пример неизмеримого множества. Манипуляции с Канторовым множеством нужны чтобы показать, что измеримость не очень хорошо взаимодействует с непрерывностью.

Но в целом я не очень хорошо понимаю, чем аксиома выбора так уж провинилась, что доказательство существования с её использованием не считается построением, а вот с использованием аксиом бесконечности или булеана множества строить можно.

В целом, я бы сказал, тут есть три категории:
1. Построенные с использованием "неконструктивных" средств. Например аксиомы выбора. В первую очередь про множества и другие объекты, которые полностью записать на бумажке всё равно невозможно.
2. Натуральные числа/строки (=конечные объекты), доказательство существования которых записать можно, но ни про какую конкретно записанную на бумажке строку доказать, что именно она удовлетворяет этому свойству, нельзя. Пример - $BB(9000)$.
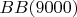
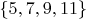
2.1. Конечные объекты, про которые неизвестно, можно ли доказать, что конкретный объект удовлетворяет нужному свойству. Пример - наименьшее число $n$ из $\{5, 7, 9, 11\}$, такое что $\zeta(n)$ иррационально.
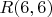
3. Конечные объекты, которые точно существуют и понятно как написать конкретный пример, но поля форума слишком узки. Пример - $R(6, 6)$.

[dsge]

mihaild в сообщении #1695618 писал(а):

В 11 примере 8 главы они строят стандартный пример неизмеримого множества.

Это тот же пример что и в Колмогорове и Фомине. С Канторовыми можествами пример 1 гл. 11.

[Shadow]

Booker48 в сообщении #1695583 писал(а):

заведомо существующие (например, доказана теорема существования), но не обнаруженные по какой-то причине

Простой делитель большого составного числа.

[sergey zhukov]

mihaild в сообщении #1695593 писал(а):

Известно, что хотя бы одно из них иррационально. Но какое конкретно (а так же одно среди них иррациональное, два, три, или все четыре) - неизвестно.

Помню, в одной книжке ставился вопрос о том, может ли иррациональное число в иррациональнрй степени быть рациональным? Тут же давалось такое доказательство:

Возьмем $\sqrt{2}^\sqrt{2}$. Что это за число? Положим, оно рационально. Тогда вот и пример, теорема доказана.

Если же оно иррационально, то возведем его еще раз в степень $\sqrt{2}$, и результат будет 2 (рациональное число), т.е. опять же теорема доказана.

Такое доказательство: неизвестно, какой из примеров истинный, но известно, что какой-то истинный.

[nnosipov]

sergey zhukov в сообщении #1695638 писал(а):

неизвестно, какой из примеров истинный

Известно: число $\sqrt{2}^{\sqrt{2}}$ трансцендентно (теорема Гельфонда).

[Anton_Peplov]

sergey zhukov
Этот пример часто приводится при обсуждении доказательств существования. Но, как уже указал nnosipov, он искусственный: на самом деле известно, какое число рационально.

Еще красивее пример, который использовал на лекциях Гильберт: «Среди вас имеется по крайней мере один студент — назовем его $X$, — в отношении которого верно следующее утверждение: ни у одного другого студента в аудитории нет на голове большего числа волос, чем у $X$. Кто этот студент? Этого мы никогда не узнаем; но в его существовании мы можем быть абсолютно уверены». (Цититирую по Кранцу). Но это не то, о чем спрашивал ТС.

[dsge]

Из теорема Борсука следует, что на поверхности Земли всегда существуют две противоположные (антиподальные) точки с абсолютно одинаковой температурой, но где эти точки находятся точно неизвестно. На самом деле даже с одинаковой температурой и давлением, две непрерывные функции на сфере.