Комбинаторика, разбиение числа

[Soul Friend]

1) Есть метод нахождения количества разбиений числа механическим способом (на бумаге), читал как-то в интернете, но сейчас не могу найти и вспомнить полностью.
Что я смутно помню:
На бумаге в столбец записываются нечетные числа, и из них помечаются квадраты чисел. Далее, на второй бумаге записываются в столбец еще какие то числа. И каждый раз, сдвигая эти две колонки чисел, суммируют каким-то определенным способом и находят точное количество разбиений числа. Кажется, метод основа на производящей функции степенных рядов. Есть ли ссылка на данный метод, или можете напомнить мне правильный алгоритм действий в этом методе ?

2) Если усложнить разбиение числа так, чтобы и одинаковые числа в разбиении тоже имели бы порядковые номера, то как считать в таком случае ? Пример на картинке :

(Картинка)

Может, правилно будет сказать - композиция числа, так как порядок учитывается.

[dgwuqtj]

1) Есть пентагональная теорема Эйлера,

$$p(n) = \sum_{0 \neq q \in \mathbb Z} (-1)^{q + 1} p(n - \frac {3 q^2 - q} 2) = \ldots + p(n - 15) - p(n - 7) + p(n - 2) + p(n - 1) - p(n - 5) + p(n - 12) - \ldots$$

при $n > 0$. Тут считается, что $p(n) = 0$ при $n < 0$.

[wrest]

Soul Friend в сообщении #1695323 писал(а):

Если усложнить разбиение числа так, чтобы и одинаковые числа в разбиении тоже имели бы порядковые номера, то как считать в таком случае ?

Вас интересует формула или алгоритм на каком-то языке?
Какие предполагаются порядки чисел?
Для числа 8 у меня получилось 47319 композиций по вашим правилам, проверьте пож-ста это то что вы хотели? Можем взять число поменьше. Для числа 4 получается 35 композиций по вашим правилам.

[Null]

2)У меня получается $2^{n-1}$

[Soul Friend]

Null
а у меня для $n=3$ получилось 8, то есть $2^n$

wrest
Можно начать с алгоритмов, потом формулы.

[wrest]

Null в сообщении #1695332 писал(а):

У меня получается $2^{n-1}$

Это у вас формула с учетом порядка следования разных, но без учета нумерации одинаковых слагаемых.
Рассмотрим композиции имени Soul Friend для $n=3$
$1_1+1_2+1_3$ дадут $3!$ перестановок
$1_1+2_1$ дадут $2!$ перестановок
$3_1$ - ну тут $1$ перестановка
Итого $3!+2!+1=6+2+1=9$
А по вашей формуле $2^{3-1}=4$

-- 25.07.2025, 09:34 --

Soul Friend в сообщении #1695333 писал(а):

Можно начать с алгоритмов, потом формулы.

Количество композиций имени Soul Friend на pari/gp, когда одинаковые слагаемые пронумерованы:

compositions(n)=my(v=partitions(n),c=0);for(i=1,#v,c+=(#v[i])!);return(c)

Работает (у меня) где-то до $n=79$, потом не хватает памяти (я выделяю pari/gp 2 гигабайта).

[Soul Friend]

wrest
Просто сумма факториалов для всех $n$ ?
Надо сравнить с реальными значениями.

[wrest]

Soul Friend в сообщении #1695337 писал(а):

Просто сумма факториалов для всех $n$ ?

Нет, не просто.

-- 25.07.2025, 09:56 --

Soul Friend в сообщении #1695337 писал(а):

Надо проверить с реальными значениями.

Конечно. Пожалуйста, проверьте для $n=4$ и $ n=5$
Пары листков бумаги должно хватить.

-- 25.07.2025, 10:30 --

dgwuqtj в сообщении #1695326 писал(а):

1) Есть пентагональная теорема Эйлера,

В практических вычислениях лучше использовать ряд Харди-Рамануджана-Радемахера, он очень быстро сходится, вычисления соответственно тоже очень быстрые. В pari/gp это реализует встроенная функция numbpart(n)

[wrest]

wrest в сообщении #1695339 писал(а):

В pari/gp это реализует встроенная функция numbpart(n)

Собсно реализация формулы Харди-Рамануджана-Радемахера в целом выглядит так (взято из исходного кода pari/gp и поправлены опечатки):

Psi(n, q) = my(a=sqrt(2/3)*Pi/q, b=n-1/24, c=sqrt(b));(sqrt(q)/(2*sqrt(2)*b*Pi))*(a*cosh(a*c)-(sinh(a*c)/c));
L(n,q)=sqrt(q/3)*sum(l=0,2*q-1,if(((3*l^2+l)/2+n)%q==0,(-1)^l*cos((6*l+1)/(6*q)*Pi)));
part(n) = round(sum(q=1,5 + 0.24*sqrt(n),L(n,q)*Psi(n,q)));

[Soul Friend]

wrest
Встроенная функция partiton(n) возвращает вектор всех разбиений числа $n$, далее, суммируются факториалы длин этих векторов. Как говорится (про код) "Краткость сестра таланта".

1) я ищу этот "механический" способ, а формулы есть в вики. Неужели он мало кому известен ?

[wrest]

Soul Friend в сообщении #1695367 писал(а):

Встроенная функция partiton(n) возвращает вектор всех разбиений числа $n$, далее, суммируются факториалы длин этих векторов.

Ну да, вы же этого и хотели?
Непонятно только как у вас "получилось"

Soul Friend в сообщении #1695333 писал(а):

а у меня для $n=3$ получилось 8, то есть $2^n$

Это догадка из космоса?
Для n=3 можно всё выписать же на листок бумаги, раскрасить и посчитать...

-- 25.07.2025, 14:46 --

Soul Friend в сообщении #1695367 писал(а):

я ищу этот "механический" способ, а формулы есть в вики. Неужели он мало кому известен ?

Тема подсчёта количества разбиений хорошо проработана, там особо новостей нет со времён Эйлера и потом Харди-Рамануджана.
Хотя с точки зрения вычислительной эффективности подсчёта изолированного $p(n)$, был очень хороший прогресс вот тут в 2012 : http://dx.doi.org/10.1112/S1461157012001088

[Soul Friend]

Да я само число 3 не посчитал.
2) A101880

[wrest]

Soul Friend в сообщении #1695375 писал(а):

2) A101880

Вот вам функция, которая очень загадочно, но при этом довольно быстро вычисляет $a(n)$ для A101880

a(n) =
  {
my(k1 = n+1, kx = k1, a = 1, t = vector(k1, i, vector(n)));
  t[k1][1] = 1;
  for (i = 1, n-1,
    my(ky = a);
    t[a] = vector(n, j, if (!(ky--), ky = k1);
                        if (j == 1, t[ky][1]
                                      , t[kx][j-1] + t[ky][j]));
    kx = a; if (a++ > k1, a = 1));
    a=if(a == 1, k1, a-1);
    return(sum(i=1,n,t[a][i]*i!));
}

a(1000) у меня вычисляется за одну секунду.
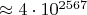
Но поля этого форума слишком узкие для результата ($\approx 4\cdot 10^{2567}$)

[wrest]

Число A101880(196) оказалось простым
А вот являются ли числа A101880(1033), A101880(1087), A101880(1522), A101880(1625) - простыми? Определить не удалось...