Цитата:
Нет, с чего Вы это взяли?
Пусть

,
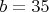
. Найдите делители

,

и

.
Понятно что Вы хотели показать: 6 - 1, 2, 3, 6; 35 - 1, 5, 7, 35; 6*35 - делители 6 и 35 а также произведения каждого с каждым, то есть, например не только первого делителя первого на первый делитель второго, но и на второй делитель второго и на третий и т.д.
Но как это чисто алгебраически получается? У нас

(Вы же под

- вели аналогию с делителем

, а не с изначальным аргументов

?) есть произведение двух

и

, которые, в свою очередь, есть произведения простых, делящих

и

соответственно, в степени, в которой они (простые) входят в разложение

,
одного и того же 
.
То есть получается, грубо
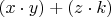
+..., и мы непонятно на основании чего утверждаем что это равно
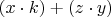
, то есть например
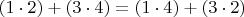
.
Я думаю, что причина моего непонимания (если в лекции всё верно) как-то связана с упусканием того факта что по определению мы суммируем все делители, а все делители представляем через простые, которые, в отличии от всех делителей не составные, и взаимно простые. Я наверное, как-то упускаю, что мы рассматриваем все делители, которые между собой могут не быть взаимно простыми, и там по нескольку раз как-то всё может умножаться.
-- 22.07.2025, 18:30 --Не очень понятно, что в формулировке Лектора имелось в виду под

и

в последующем, при доказывании сумм. Это именно составляющие одного конкретного

, как я это понял и описал выше, или что-то другое, более "сквозное"
-- 22.07.2025, 18:41 --Каждый

каждого

умножается на каждый

каждого

и это всё складывается, то есть (верхний индекс - принадлежность к n-ому делителю

, а не степень)
Если вы пронумеровали через

все делители

, то неверно, что

пробегает все делители

по одному разу. Есть биекция между делителями
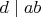
и парами
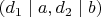
.
"Пробегает" там только

каждого

по

каждого

. То есть, если хотите, имеется неинъективная сюръекция из множества "дэ вторых", сформированных из каждого

в

первого

. И такая сюръекция на каждый "дэ первый" приходится. Это в случае выражений с двойными суммами. По крайней мере если я так понимаю, что имеется в виду под двойной суммой.
А в первом выражении, с одной суммой, там действительно биекция - каждому

соответствует один

из того же

.