Разбиение области на элементарные

[Rammstein]

Здравствуйте! В нашем курсе матанализа даются следующие определения:
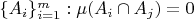
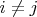
1. Разбиением измеримого множества A называется конечный набор измеримых множеств $\{A_i\} _{i=1}^m: \mu(A_i \cap A_j) = 0$ при $ i \ne j$ и $\cup A_i = A$
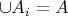
2. Область - открытое связное множество
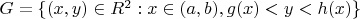
3, 4. Элементарная область относительно OY - та, которую можно представить в виде $G = \{(x, y) \in R^2: x \in (a, b), g(x) < y < h(x)\}$, где g и h непрерывно дифференцируемы на [a, b]. Для OX аналогично.
Вопрос: существует ли в данной терминологии область, не являющаяся элементарной, но допускающая разбиение как на конечное число областей, элементарных относительно OY, так и на конечное число областей, элементарных относительно OX?
Если да, то приведите пример. Вся проблема возникает из-за открытости областей. Я рассматривал кольцо между окружностями радиуса 1 и 2 с центрами в начале координат. Если разделить его на 4 части по квадрантам, то из-за их открытости они не покроют всё кольцо(отрезки осей координат не лежат в объединении), а значит, не будут являться разбиением.

[vpb]

Вы путаете условия $A_i\cap A_j=\emptyset$ и $\mu(A_i\cap A_j)=0$, похоже.

[mihaild]

vpb в сообщении #1694731 писал(а):

$A_i\cap A_j=\emptyset$ и $\mu(A_i\cap A_j)=0$

Для открытых множеств это одно и то же.
В связи с чем вместе с

Rammstein в сообщении #1694728 писал(а):

Область - открытое связное множество

возникают некоторые проблемы с любым разбиением области на области (более чем на одну область).

[vpb]

Значит, или задача неправильно приведена, или это специально задача с запутыванием.