Первый вопрос: а чему, по-Вашему, равен предел
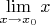
?
 -- 17.07.2025, 08:04 --
-- 17.07.2025, 08:04 --Solaris86, то, что Вы написали, - это определение непрерывной в точке

функции. Правда, несколько вычурное. Обычно пишут проще: функция

непрерывна в точке

, если
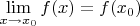
.
Для произвольной функции

и произвольной точки

Ваше равенство неверно.
Это фрагмент из книги "Конспект лекций по высшей математике" Д.Т. Письменного

Для меня тут непонятна именно
последовательность рассуждения: если бы было написано, что так как
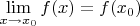
, а
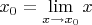
и, соответственно,
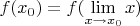
, то
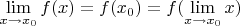
. Понятно, если через такую цепочку рассуждений приходим к выводу, что
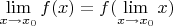
, так как каждая из частей этого равенства равна

и это

является связующим.
В книге же другая
последовательность рассуждения:
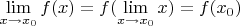
, тут связующим получается
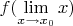
, поэтому у меня и возник вопрос: а как при этом доказать, что
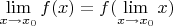
.