Доказательство 5-го постулата Евклида

[epros]

Konstantin12 в сообщении #1694413 писал(а):

Я не пытаюсь ввести постулат, о сумме углов в треугольнике.
Я пытаюсь это доказать не опираясь на 5-й постулат.
В качестве основы использую свойство прямой, проведенной через центр окружности, делить эту окружность пополам.

Это свойство окружности делиться пополам - это новый предлагаемый Вами постулат что ли?

Не сработает так. Потому что на сфере, например, это свойство выполняется, но сумма углов треугольников не всегда равна 180 градусам и геометрия неевклидова.

[Konstantin12]

dgwuqtj в сообщении #1694440 писал(а):

Konstantin12 в сообщении #1694413 писал(а):

Может они таки складываются, только проблема с суммой углов в том же треугольнике в чем то другом?
Может проблема с углами между отрезками на прямой?
Как думаете?

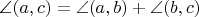
....Если это дело обобщать на прямые, не пересекающиеся в общей точке, то утверждение, что $\angle(a, c) = \angle(a, b) + \angle(b, c)$ в смысле мер соответствующих углов уже буквально равносильно утверждению о сумме углов треугольника (и "пятому постулату"). То есть углы между $a$ и $b$, а также между $b$ и $c$, нельзя просто сложить, чтобы найти угол между $a$ и $c$. Я писал именно об этом.

Вы угол между отрезками определяете как угловую меру угла между прямыми, содержащими эти отрезки. То есть строим прямые, находим точку пересечения (если она есть; если она не единственная, её ещё надо выбрать), выбираем лучи с этой вершиной в данных прямых и считаем меру одного из образовавшихся углов. Если отрезки на одной прямой, то всегда будет угловая мера $0^\circ$, $180^\circ$ или $360^\circ$ в зависимости от сделанных выборов. Это верно и в евклидовой геометрии, и в геометрии Лобачевского, и в сферической, и в геометрии Римана.

Конечно тяжеловато понимать написанное без рисунков (в частности вот это "если она не единственная, её ещё надо выбрать")
Но, по-моему я понял и согласен с такими утверждениями.

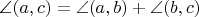
То что "утверждение, что $\angle(a, c) = \angle(a, b) + \angle(b, c)$ в смысле мер соответствующих углов уже буквально равносильно утверждению о сумме углов треугольника (и "пятому постулату")",
с этим тоже не спорю.
Единственная деталь, которая позволяет уйти от 5-го постулата - это фиксация углов между отрезками на прямой (запрет кривизны прямой.)

Вот что представляет из себя Орицикл Лобачевского (окружность бесконечного радиуса на плоскости) и поведение прямых внутри его.

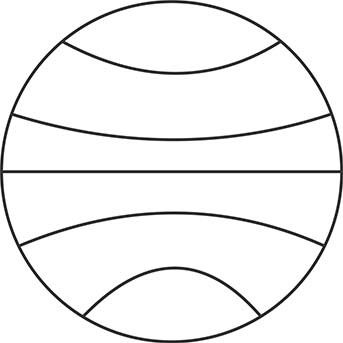
Все прямые пересекаются с Орициклом под прямым углом. В том числе и прямая проходящая через центр Орицикла.
Это прямая, кроме того делит Орицикл пополам, потому что Лобачевский не отрицал 17-го определения Евклида (О прямой проходящей через центр окружности).
Из этого рисунка можно понять, что если поворачивать прямую проходящую через центр Орицикла, эта прямая не перестанет делить Орицикл пополам.
Отсюда следует, что мы можем взять любую окружность с заранее заданным размером радиуса (т.е. меньше бесконечного) и поместить ее в любую точку плоскости. Прямая проходящая через центр нашей окружности, всегда будет делить эту окружность пополам.

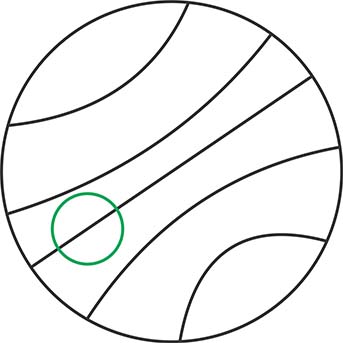
И вот мы подходим к узкому месту у Лобачевского.
Для того чтобы сумма углов в любом треугольнике была меньше 180 градусов, мы должны ввести абсолютный, фиксированный, центр Бесконечного Орицикла на плоскости. Здесь, на мой взгляд, есть логическое противоречие. Как на плоскости найти фиксированный центр бесконечного круга? Его, на мой взгляд, не должно существовать.
Тем более, и Лобачевский, и другие критики Евклида, как до Лобачевского, так и после него, не спорили с 17-м определением Евклида, что прямая, проходящая через центр круга делит его пополам. Заметьте, любая прямая и центр любой окружности. Т.е. нет фиксированных мест на плоскости.

Отсюда, можно заключить, что угол между любыми отрезками на прямой равен нулю. Т.е. при каком угодно удалении отрезков на прямой угол между ними не изменяется (всегда равен нулю градусов). Соответственно, сумма углов в треугольнике любого размера равен 180 градусов., потому что максимальный поворот радиуса круга равен 360 градусов.
Тем самым, мы подтверждаем 5-постулат. Заметьте, подтверждаем, но не используем в определении суммы углов в треугольнике.

[Geen]

Konstantin12 в сообщении #1694413 писал(а):

В качестве основы использую свойство прямой, проведенной через центр окружности, делить эту окружность пополам

А есть такой постулат? Если нет, то надо доказывать. Причём, строго.

[Konstantin12]

epros в сообщении #1694445 писал(а):

Konstantin12 в сообщении #1694413 писал(а):

Я не пытаюсь ввести постулат, о сумме углов в треугольнике.
Я пытаюсь это доказать не опираясь на 5-й постулат.
В качестве основы использую свойство прямой, проведенной через центр окружности, делить эту окружность пополам.

Это свойство окружности делиться пополам - это новый предлагаемый Вами постулат что ли?

Нет, это 17-е определение Евклида. Неоспариваемое никем.

epros в сообщении #1694445 писал(а):

Не сработает так. Потому что на сфере, например, это свойство выполняется, но сумма углов треугольников не всегда равна 180 градусам и геометрия неевклидова.

Речь о геометрии на плоскости (не о геометрии на сфере, не о сферической геометрии). Я уже это говорил.

-- 16.07.2025, 15:18 --

Geen в сообщении #1694479 писал(а):

Konstantin12 в сообщении #1694413 писал(а):

В качестве основы использую свойство прямой, проведенной через центр окружности, делить эту окружность пополам

А есть такой постулат? Если нет, то надо доказывать. Причём, строго.

Есть. Только не постулат, а 17-е определение.
Никто его не оспаривает.

Простое логическое рассуждение. Какую из половин окружности выберете? Есть критерий выбора?

[Geen]

Konstantin12 в сообщении #1694481 писал(а):

Простое логическое рассуждение. Какую из половин окружности выберете? Есть критерий выбора?

Северную.
Это "рассуждение" к логике не имеет отношения.

Konstantin12 в сообщении #1694481 писал(а):

Нет, это 17-е определение Евклида.

Определение чего? Окружности? Прямой? Проходящей через центр?

-- 16.07.2025, 15:23 --

Konstantin12 в сообщении #1694481 писал(а):

Речь о геометрии на плоскости (не о геометрии на сфере, не о сферической геометрии).

Определите "геометрию на плоскости" без использования "пятого постулата".

[epros]

Konstantin12 в сообщении #1694481 писал(а):

Речь о геометрии на плоскости (не о геометрии на сфере, не о сферической геометрии). Я уже это говорил.

Ничего не знаю ни про какую плоскость. Предъявляйте набор аксиом и выводы будем делать только на их основании. Аксиомы "это не на сфере" у нас нет и быть не может.

-- Ср июл 16, 2025 16:55:47 --

Konstantin12 в сообщении #1694475 писал(а):

Отсюда, можно заключить, что угол между любыми отрезками на прямой равен нулю. Т.е. при каком угодно удалении отрезков на прямой угол между ними не изменяется (всегда равен нулю градусов). Соответственно, сумма углов в треугольнике любого размера равен 180 градусов

Допустим, что Вы определите угол между двумя направлениями, проведёнными из разных точек, как разницу углов между этими направлениями и прямой, соединяющей эти точки. Но отсюда равенство суммы углов треугольника 180 градусам никак не следует.

[dgwuqtj]

Konstantin12 в сообщении #1694475 писал(а):

Вот что представляет из себя Орицикл Лобачевского

Обычно это называют абсолютом. Орициклы — это специальные кривые внутри него.

Konstantin12 в сообщении #1694475 писал(а):

Это прямая, кроме того делит Орицикл пополам, потому что Лобачевский не отрицал 17-го определения Евклида (О прямой проходящей через центр окружности).

Абсолют — это не окружность, у него вообще нет точек в самой геометрии Лобачевского. Это как бесконечно удалённая прямая для евклидовой плоскости.

Konstantin12 в сообщении #1694475 писал(а):

мы должны ввести абсолютный, фиксированный, центр Бесконечного Орицикла на плоскости.

Зачем? Любая прямая геометрии Лобачевского делит абсолют "пополам". Вот только на абсолюте нет длины, и если его как-то поделить пополам, то всегда можно поделить по-другому так, чтобы строго уменьшить одну из частей.

[Konstantin12]

Geen в сообщении #1694483 писал(а):

Konstantin12 в сообщении #1694481 писал(а):

Простое логическое рассуждение. Какую из половин окружности выберете? Есть критерий выбора?

Северную.

Какой критерий?

Geen в сообщении #1694483 писал(а):

Это "рассуждение" к логике не имеет отношения.

Konstantin12 в сообщении #1694481 писал(а):

Нет, это 17-е определение Евклида.

Определение чего? Окружности? Прямой? Проходящей через центр?

Откройте "Начала" Евклида, узнаете.

-- 16.07.2025, 15:23 --

Geen в сообщении #1694483 писал(а):

Konstantin12 в сообщении #1694481 писал(а):

Речь о геометрии на плоскости (не о геометрии на сфере, не о сферической геометрии).

Определите "геометрию на плоскости" без использования "пятого постулата".

Можете посмотреть у Лобачевского.

[Booker48]

Konstantin12 в сообщении #1694496 писал(а):

Откройте "Начала" Евклида, узнаете.

Напрасно вы на Евклида ссылаетесь, повторюсь. Слишком архаичный текст, если открыть примечания к книге 1, то там сказано, как тот же Ламберт (четырёхугольник которого вы, кстати, используете в своём доказательстве) относился к этим определениям ещё в XVIII веке. Нормальное доказательство должно опираться на современные аксиоматики. Коих много.

[Konstantin12]

dgwuqtj в сообщении #1694495 писал(а):

Konstantin12 в сообщении #1694475 писал(а):

Вот что представляет из себя Орицикл Лобачевского

Обычно это называют абсолютом. Орициклы — это специальные кривые внутри него.

Konstantin12 в сообщении #1694475 писал(а):

Это прямая, кроме того делит Орицикл пополам, потому что Лобачевский не отрицал 17-го определения Евклида (О прямой проходящей через центр окружности).

Абсолют — это не окружность, у него вообще нет точек в самой геометрии Лобачевского. Это как бесконечно удалённая прямая для евклидовой плоскости.

Обычно, я стараюсь читать оригинал, а не интерпретаторов и комментаторов на изучаемый предмет.
Вот что пишет Лобачевский в своих "Геометрических исследованиях по теории параллельных линий":
"31) Предельной линией (орициклом) мы называем такую расположенную в плоскости кривую линию, у которой все перпендикуляры, восстановленные из середины ее хорд, параллельны между собой.
32) Круг, радиус которого возрастает, переходит в предельную линию."
Цифры вначале строк - это номера Предложений по Лобачевскому.

dgwuqtj в сообщении #1694495 писал(а):

Konstantin12 в сообщении #1694475 писал(а):

мы должны ввести абсолютный, фиксированный, центр Бесконечного Орицикла на плоскости.

Зачем? Любая прямая геометрии Лобачевского делит абсолют "пополам". Вот только на абсолюте нет длины, и если его как-то поделить пополам, то всегда можно поделить по-другому так, чтобы строго уменьшить одну из частей.

Если мы не зафиксируем центр Орицикла, тогда я могу при каждом построении прямой выбирать его (центр) так, что эта прямая, мной выбранная будет делить окружность пополам. Тогда я смогу накладывать эту прямую на сторону треугольника и утверждать, что любые отрезки на ней (стороне треугольника) будут между собой иметь угол равный нулю.

Честно говоря не хочется погружаться в эту "кроличью нору" (поиски ошибок у Лобачевского), т.к. это не имеет отношение к моему доказательству. Я не использую геометрию Лобачевского, не опровергаю ее как этап в своих рассуждения. Я опираюсь на 17-е определение Евклида. А геометрия Лобачевского мне была нужна, чтобы понять источник проблемы с прямыми линиями.

-- 16.07.2025, 18:06 --

Booker48 в сообщении #1694499 писал(а):

Konstantin12 в сообщении #1694496 писал(а):

Откройте "Начала" Евклида, узнаете.

Напрасно вы на Евклида ссылаетесь, повторюсь. Слишком архаичный текст, если открыть примечания к книге 1, то там сказано, как тот же Ламберт (четырёхугольник которого вы, кстати, используете в своём доказательстве) относился к этим определениям ещё в XVIII веке. Нормальное доказательство должно опираться на современные аксиоматики. Коих много.

Я ссылаюсь на Евклида, так как это самый простой вариант указать источник о котором все слышали и который перемолот вдоль и поперек. И в этом источнике есть нужное мне, и никем не оспариваемое утверждение/определение.
Перебирать современную аксиоматику, чтобы найти это же утверждение, которое есть у Евклида? Зачем? Так моднее?

[Booker48]

Konstantin12 в сообщении #1694501 писал(а):

Я ссылаюсь на Евклида, так как это самый простой вариант указать источник о котором все слышали и который перемолот вдоль и поперек. И в этом источнике есть нужное мне, и никем не оспариваемое утверждение/определение.
Перебирать современную аксиоматику, чтобы найти это же утверждение, которое есть у Евклида? Зачем? Так моднее?

Ну, вы же видите, как и здесь, и на хабре относятся к такого рода доказательствам? Опирающимся на текст, сомнительный с точки зрения даже не современной, а 300-летней давности (Ламберт, Саккери) строгости?
Евклид - он, конечно, памятник, его не посадят осудят, но он же разобран-переразобран. Современные аксиоматики не с потолка свалились и не богом ниспосланы на скрижалях.
Обсуждение зациклилось, не заметили? Вы говорите - 17е определение, а вам отвечают - докажите его нормальным образом.
Но уже несколько сотен лет назад очень похожие на ваше доказательства имели место (см. "Четырехугольник Саккери", "Четырехугольник Ламберта" в вики) - и были отвергнуты примерно тогда же.

[dgwuqtj]

Konstantin12 в сообщении #1694501 писал(а):

Предельной линией (орициклом) мы называем такую расположенную в плоскости кривую линию, у которой все перпендикуляры, восстановленные из середины ее хорд, параллельны между собой.

Замечательно, только у вас не орицикл, а абсолют. Орицикл состоит из точек самой геометрии, откройте хоть Википедию и посмотрите картинки.

Konstantin12 в сообщении #1694501 писал(а):

Круг, радиус которого возрастает, переходит в предельную линию.

А в евклидовой геометрии окружность при возрастании радиуса стремится к прямой. Но не при любом возрастании радиуса, а если, скажем, зафиксировать её точку и касательную в этой точек. Если увеличивать радиусы концентрических окружностей, то в пределе будет вообще пустое множество (не считая бесконечно удалённых точек, конечно, которые в самой геометрии не лежат). Тут под предельной линией понимается орицикл в обычном смысле, а не что вы там надумали.

Konstantin12 в сообщении #1694501 писал(а):

Тогда я смогу накладывать эту прямую на сторону треугольника и утверждать, что любые отрезки на ней (стороне треугольника) будут между собой иметь угол равный нулю.

Не можете утверждать, это логически ниоткуда не следует.

Konstantin12 в сообщении #1694501 писал(а):

Перебирать современную аксиоматику, чтобы найти это же утверждение, которое есть у Евклида? Зачем? Так моднее?

Так строже. У Евклида куча результатов строго не выводятся из основных предположений. А с современной аксиоматикой можно чисто механически находить пробелы и ошибки в рассуждениях. Даже картинки не нужны, хотя с ними и удобнее.

-- 16.07.2025, 18:25 --

Konstantin12 в сообщении #1694413 писал(а):

Вот как я вижу проблему с углами между отрезками:

Возьмите модель Клейна, что ли...

[Geen]

Konstantin12 в сообщении #1694496 писал(а):

Откройте "Начала" Евклида, узнаете.

Скан оригинала приложите, пожалуйста....

[Konstantin12]

Booker48 в сообщении #1694505 писал(а):

Konstantin12 в сообщении #1694501 писал(а):

Я ссылаюсь на Евклида, так как это самый простой вариант указать источник о котором все слышали и который перемолот вдоль и поперек. И в этом источнике есть нужное мне, и никем не оспариваемое утверждение/определение.
Перебирать современную аксиоматику, чтобы найти это же утверждение, которое есть у Евклида? Зачем? Так моднее?

....
Обсуждение зациклилось, не заметили? Вы говорите - 17е определение, а вам отвечают - докажите его нормальным образом.

Доказательство определения? Вы серьезно?
Может еще доказать, что прямой угол равен 90 градусов?
17-е определение Евклида - это определение, что такое Диаметр. Евклид определяет его как прямую проходящую через цент окружности и делящий окружность пополам.
В издании "Начал" Евклида от 1950 года чуть ли не половина первых 6 томов отдана под комментарии. В том числе много комментариев по поводу определений Евклида, с упоминанием авторов живших до этого издания.
И ни одного комментария по поводу 17-го определения (определения Диаметра круга).
Видимо всем комментаторам жившим до 1950 года показалось это определение настолько бесспорным и очевидным, что никто не нашел что-либо сказать по этому поводу.
А здесь требуют доказать.
Смешно.

-- 17.07.2025, 01:49 --

Geen в сообщении #1694512 писал(а):

Konstantin12 в сообщении #1694496 писал(а):

Откройте "Начала" Евклида, узнаете.

Скан оригинала приложите, пожалуйста....

смешно.

[Booker48]

Konstantin12 в сообщении #1694553 писал(а):

Доказательство определения? Вы серьезно? ...
17-е определение Евклида - это определение, что такое Диаметр. Евклид определяет его как прямую проходящую через цент окружности и делящий окружность пополам.

Ну да, данное определение постулирует существование объекта с двумя свойствами. Это само по себе требует доказательства. У Евклида его нет, хотя оно возможно без пятого постулата (ПП).

Konstantin12 в сообщении #1694553 писал(а):

В издании "Начал" Евклида от 1950 года чуть ли не половина первых 6 томов отдана под комментарии. В том числе много комментариев по поводу определений Евклида, с упоминанием авторов живших до этого издания.
И ни одного комментария по поводу 17-го определения (определения Диаметра круга).
Видимо всем комментаторам жившим до 1950 года показалось это определение настолько бесспорным и очевидным, что никто не нашел что-либо сказать по этому поводу.

Вы просто не в курсе. Первый выпуск "Историко-математических исследований" вышел в 1948 году и содержит статью Болтянского про Евклида, как раз по поводу выхода нового перевода. Болтянский участвовал в работе над 3-хтомником, и написал статью, защищающую Евклида от многочисленных критиков. Разбор претензий к 17 определению там тоже есть.

Konstantin12 в сообщении #1694553 писал(а):

Может еще доказать, что прямой угол равен 90 градусов?

В правильном направлении мыслите. Вы в своём доказательстве используете как факт существование четырёхугольника, все углы которого - прямые. Но это - переформулировка ПП. И вы не докажете это утверждение, пользуясь аксиомами из "Начал" (не используя ПП). Вас и призывают чётко указывать аксиомы, которыми вы пользуетесь при доказательстве (евклидовские из "Начал" существенно неполны, но пусть). Но вы, отчего-то, считаете это отцеживанием комара.