Продолжу. Привели к вычислению положительных значений у приведенного многочлена
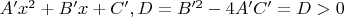
в точках
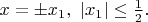
Можем считать, что
![$x_1\in [0.\frac{1}{2}]$ $x_1\in [0.\frac{1}{2}]$](https://dxdy-03.korotkov.co.uk/f/e/c/0/ec0c0fe1b1b8e0ecd0ff1c67e3cfb05882.png)
.
Рассмотрим вначале случай
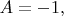
(

согласно условию задачи).
В этом случае приведенными многочленами с целыми коэффициентами
являются только
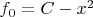
"
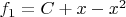
(с вершиной в интервале (0,1)).
Максимальное значение
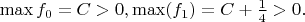
В любом случае для целочисленного многочлена

.
При целых
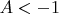
и заданных

и

не всегда существует многочлен
с целыми коэффициентами и с условием
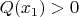
.
В этом случае длина интервала положительных значений
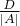
мало.
Пусть
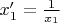
.
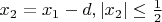
.
При этом получим опять два значения

у приведенного многочлена с тем же дискриминантом.
Переходим вначале с интервала (0,1) к
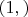
получим многочлен $-(A'+B'y+C'y^2) с отрицательным старшим коэффициентом.
Если бы коэффициент
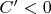
, то из
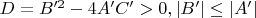
получили бы
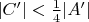
, т.е. учтенный уже в более раннем этапе.
Так получим новые 2 приведенных многочлена, у которых

отличаются только знаком. Их значения надо учитывать умножая на

У приведенных многочленов
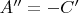
. C учетом этого к сумме Цагира
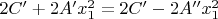
(в первом раунде) прибавится
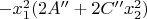
и сумма во втором раунде станет
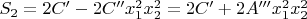
.
Добавка к
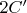
стремится к нулю из-за экспоненциального убывания поправки.
Для тех кто знаком с автоморфными формами можно показать, что сумма Цагира

является автоморфной формой степени 2 и даже параболической, соответственно (согласно теории постоянна), т.е. зависит только от параметра

.
Для дискриминанта

получим
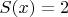
. Расчеты для других

можно вычислить по указанному выше алгоритмы.
Для старших степеней Эта сумма уже не является постоянной и вычисление гораздо сложнее.