Для начала.
Пусть

-- конечномерные линейные пространства над

.
Через

обозначим линейное пространство билинейных функций

.
Определение.
1) Тензорным произведением пространств

называется пространство

-- сопряженное к

. Оно обозначается

.
2) Тензорным произведением элементов

называется элемент

, который определен следующим образом:
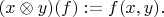
Теорема. Пусть

-- базис в

, а

-- базис в

. Тогда

-- базис в

.
(Оффтоп)
Доказательство. Множество

состоит из

элементов, при этом

Покажем, что элементы

линейно независимы. Действительно, приравняем к нулю линейную комбинацию

Пусть

-- взаимные базисы в

и

соответсвенно:

Введем билинейные функции

Тогда

Теорема доказана.
Определение. Тензором типа

(

раз контравариантным и

раз ковариантным) на пространстве

называется элемент тензорного произведения

в этом произведении

штук пространств

и

штук пространств

.
-- 29.05.2025, 22:31 --Зачем так сложно? -- Затем, что тензорное произведение это способ из билинейных отображений делать линейные.
Действительно, обозначим через

отображение

. Пусть

-- билинейное отображение в какое-нибудь линейное пространство

. Тогда существует и при том единственное линейное отображение

такое, что

