Существует ли последовательность

аналитических в некоторой ограниченной области

функций, обладающих следующими свойствами: 1)

сходится локально равномерно (= равномерно на любом компакте

) к некоторой функции
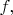
2) хотя бы для одного континуума (=связного компакта)

и одного числа

выполнено

при всех

3) никакая подпоследовательность

не сходится равномерно в области

к функции

Если ответ "да", то ещё дополнительный вопрос: существуют ли такие последовательности в (более узком) классе конформных отображений?