Рассмотрим непустые множества

,

:

.
Если

, то

,

.
Если
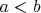
, то обозначим отрезок
![$[a_0, b_0] = [a, b]$ $[a_0, b_0] = [a, b]$](https://dxdy-04.korotkov.co.uk/f/3/9/4/394e79e9f459727a6a9e6e82ca36a98782.png)
. Разделим этот отрезок на две части:
![$[a_0, \frac{a_0 + b_0}{2}]$ $[a_0, \frac{a_0 + b_0}{2}]$](https://dxdy-01.korotkov.co.uk/f/8/f/c/8fcca44c303cf7071ea3758527946b9382.png)
и
![$[\frac{a_0 + b_0}{2}, b_0]$ $[\frac{a_0 + b_0}{2}, b_0]$](https://dxdy-04.korotkov.co.uk/f/b/3/1/b310d2faf63654da3c2747e9cdcfb95982.png)
. Если точка

принадлежит одновременно двум множествам или, наоборот, не принадлежит ни одному из множеств

, то это искомая точка

.
В противном случае из двух отрезков выбираем тот, который содержит точки обоих множеств

.
Далее повторяем описанные шаги. Процесс или будет обрываться с нахождением точки

, либо продолжаться бесконечно: пусть определен отрезок

, тогда
![$[a_k+1,b_k+1] = \begin{cases}
[a_k, \frac{a_k + b_k}{2}],& \text{если этот отрезок содержит элементы обоих множеств A, B}\\
[\frac{a_k + b_k}{2}, b_k],&\text{если этот отрезок содержит элементы обоих множеств A, B}
\end{cases}$ $[a_k+1,b_k+1] = \begin{cases}
[a_k, \frac{a_k + b_k}{2}],& \text{если этот отрезок содержит элементы обоих множеств A, B}\\
[\frac{a_k + b_k}{2}, b_k],&\text{если этот отрезок содержит элементы обоих множеств A, B}
\end{cases}$](https://dxdy-01.korotkov.co.uk/f/0/5/2/052267b67e5342c79a0207de1ef7e18082.png)
Непонятно, что с этим делать дальше.