Тривиум Арнольда, задача 10

[nnosipov]

Вчера просматривал "Математический тривиум" В.И. Арнольда и случайно взглядом наткнулся на задачу

10. Исследовать асимптотики решений $y$ уравнения $x^5+x^2y^2=y^6$, стремящихся к $0$ при $x \to 0$.

В последнее время у меня появилась скверная привычка: при встрече с уравнением с двумя неизвестными начинаю его решать в целых числах (независимо от оригинальной задачи; особенно привлекают внимание коротенькие трех-четырехчленные уравнения с небольшими коэффициентами). В принципе, для окружающих это безвредно (если, конечно, потом мне не захочется кому-то рассказать свое решение, но этим я стараюсь не злоупотреблять). Короче, вот задача:

Докажите, что уравнение $x^5+x^2y^2=y^6$ в целых числах имеет единственное решение $(0,0)$.

Она совсем простая, но в конце нас ожидает встреча с прекрасным одним старинным сюжетом, если вдруг мы захотим чего-то погорячее типа решить данное уравнение в рациональных числах. В общем, все как Арнольд любит. Вот любопытно: знал ли он об этом сюжете? Судя по брошюре "Группы Эйлера и арифметика геометрических прогрессий" ( М.: МЦНМО, 2003), теория чисел ему была интересна.

Кстати, об оригинальной задаче: команда в Maple

with(algcurves):puiseux(RootOf(x^5+x^2*y^2-y^6,y),x=0,10);

моментально выдает (довольно содержательный) ответ, но, мне кажется, голыми руками (и методом Ньютона) его тоже можно получить за разумное время --- помогает специфическая зависимость от $y$.

[drzewo]

в оригинальной задаче достаточно параметризовать кривую подстановкой $x=ty^2$

[nnosipov]

drzewo
А у Вас все в порядке с формулами? Вообще, это хорошая идея --- заметить, что относительно переменных $u=x^3$, $v=y^6$ уравнение будет задавать рациональную кривую. Но проверка показывает (я решил проверить), что на самом деле получается эллиптическая кривая относительно $(u,v)$.

Да, вот теперь все ОК, рациональная кривая будет относительно $u=x^2$, $v=y^4$.

[drzewo]

я не знаю, что такое рациональная кривая, я по мужицки:

$$x=t\sqrt{\frac{1-t^2}{t^5}},\quad y^4=\frac{1-t^2}{t^5}$$

дальше вычисляем из первого уравнения асимптотики $x$ при $t\to 1-0;\quad -1-0;\quad -\infty$
и подставляем во второе уравнение
надеюсь не проврался в арифметике, вообщем мысль понятна

[nnosipov]

drzewo в сообщении #1657693 писал(а):

я не знаю, что такое рациональная кривая

Уверен, что знаете: это кривая, допускающая параметризацию в рациональных функциях от параметра, всего лишь.

А я хотел все-таки по Ньютону, предварительно заменив $y^2$ на новый $y$ (тогда будут только тейлоровские разложения в окрестности $x=0$; потом из каждого из них --- а их будет целых три штуки, если верить Maple --- нужно еще извлечь квадратный корень, и получим ответ в виде трех разложений по полуцелым степеням $x$).

[Утундрий]

Формулы Кардано применять "не спортивно"?

[nnosipov]

Утундрий
Попробуйте :) Там же в окрестности $x=0$ без комплексных чисел не обойтись. Разве что решать кубическое уравнение в тригонометрическом виде, но это то еще удовольствие, там будут очень громоздкие выражения. Либо это превратится в задачу по ТФКП, с изучением точек ветвления многозначной аналитической функции. Вообще мрак.

[drzewo]

(Оффтоп)

Эта ситуация имеет некоторую аналогию в дифференциальных уравнениях. Как правило даже если уравнение интегрируется в квадратурах то от этих квадратур головной боли больше чем толку, а толк есть от качественного исследования дифференциального уравнения, которое, как правило, проще и информативнее.
Типичный пример это математический маятник. Уравнения движения интегрируются в эллиптических интегралах, которые надо обращать что бы получить решение как функцию времени. При этом фазовый портрет маятника рисуется просто и независимо от этих интегралов и дает полную качественную картину поведения системы.

[nnosipov]

drzewo в сообщении #1657731 писал(а):

Как правило даже если уравнение интегрируется в квадратурах то от этих квадратур головной боли больше чем толку

Готов поверить на слово, здесь у меня опыта очень мало.

Я все-таки напишу, как можно было бы решить задачу Арнольда методом Ньютона (сейчас прикинул на бумажке, там совсем крохотные вычисления, можно студентам прямо на экзамене давать). Итак, имеем уравнение $x^5+x^2y-y^3=0$ (это новое $y$, которое равно квадрату старого $y$), при этом $y(0)=0$. Пусть $y=kx^\varepsilon+o(x^\varepsilon)$ при $x \to 0$, при этом $\varepsilon>0$ и $k \neq 0$. Подставив в уравнение, получим

$$L(x)=x^5+kx^{2+\varepsilon}+o(x^{2+\varepsilon})-k^3x^{3\varepsilon}+o(x^{3\varepsilon})=0.$$

Далее рассмотрим случаи.
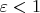
1) $\varepsilon<1$. Здесь $2+\varepsilon>3\varepsilon$, поэтому $L(x)=-k^3x^{3\varepsilon}+o(x^{3\varepsilon})$ и не может быть тождественным нулем. Значит, этот случай невозможен.
2) $\varepsilon=1$. Тогда $L(x)=(k-k^3)x^3+o(x^3)$, откуда $k-k^3=0$ (иначе противоречие), т.е. $k \in \{-1,1\}$. Тем самым, найдены два решения: $y=-x+o(x)$ и $y=x+o(x)$.
3) $\varepsilon>1$. Тогда $2+\varepsilon<3\varepsilon$. Покажем, что единственным возможным значением может быть $\varepsilon=3$. Действительно, если $\varepsilon<3$, то $L(x)=kx^{2+\varepsilon}+o(x^{2+\varepsilon})$, а если $\varepsilon>3$, то $L(x)=x^5+o(x^5)$. Если же $\varepsilon=3$, то $L(x)=(1+k)x^5+o(x^5)$, откуда $k=-1$. Вот и третье решение: $y=-x^3+o(x^3)$.

Теперь для каждой ветви можно вычислять следующие члены разложения. Например, пусть $y=x+kx^\varepsilon+o(x^\varepsilon)$. Здесь в том же духе придется чуть подольше считать (желающие могут попробовать), в итоге получим $\varepsilon=3$ и $k=1/2$, т.е. $y=x+\frac{1}{2}x^3+o(x^3)$.

-- Пн окт 07, 2024 17:54:10 --

(Оффтоп)

drzewo в сообщении #1657731 писал(а):

Уравнения движения интегрируются в эллиптических интегралах, которые надо обращать что бы получить решение как функцию времени.

Нашел у себя подобный пример: движение шарика по желобу в виде полуокружности под действием силы тяжести.

[drzewo]

Гм, кажется у меня получается что-то другое. Положим $t=-s,\quad s\to\infty$ тогда

$$x=-s\sqrt{\frac{1-s^2}{-s^5}}\Longrightarrow x=-\frac{1}{\sqrt s}(1+o(1))\quad \mbox{и} \quad x<0\Longrightarrow s=\frac{1}{x^2}(1+o(1))$$

Далее

$$y^4=\frac{1-s^2}{-s^5}=\frac{1}{s^3}(1+o(1))\Longrightarrow |y|=(-x)^{3/2}(1+o(1))$$

[nnosipov]

drzewo в сообщении #1657749 писал(а):

Гм, кажется у меня получается что-то другое.

Да ровно то же самое, для третьего решения: квадрат вашего $y$ есть мой $y$ (обратите внимание, что у меня все выкладки делаются для уравнения $x^5+x^2y-y^3=0$, а оригинальное уравнение $x^5+x^2y^2-y^6=0$).

[drzewo]

понятно

[lel0lel]

nnosipov в сообщении #1657681 писал(а):

Докажите, что уравнение $x^5+x^2y^2=y^6$ в целых числах имеет единственное решение $(0,0)$.

Видно, что целые $x, y$ имеют равные радикалы. Предположим, что нетривиальное решение есть. Пусть простое $p$ делит $x$, тогда $p^{5a}x_1^5+p^{2a+2b}x_1^2y_1^2=p^{6b}y_1^6$, где $x_1, y_1$ не делятся на $p$. Показатели $5a,2a+2b,6b$ не могут быть различными, иначе, не пройдём сравнение по степени $p$ c показателем средней величины. Показатели не могут быть равными, так как это приводит к $a=b=0$. Остаются случаи когда только два из трёх показателя равны.
1) Если $5a=2a+2b$, то $b=3/2a$ и уравнение приводится к $x_1^5+x_1^2y_1^2=p^{4a}y_1^6$;
2) $5a=6b<2a+2b$ быть не может, так как $5a+6b<4a+4b$ не выполняется для натуральных чисел;
3) Если $6b=2a+2b$, то $b=1/2a$ и уравнение приводится к $p^{2a}x_1^5+x_1^2y_1^2=y_1^6$;
Если перебрать все простые, то придём к уравнению вида $\pm m^2+1=n^4$, где $m n=x$. Это уравнение не имеет решений.

[nnosipov]

lel0lel
Спасибо. Я предполагал вот такое рассуждение. Положив $y^2=z$, получим уравнение $x^5+x^2z-z^3=0$, которое и будем решать в целых числах. Считая $x \neq 0$ и $z \neq 0$, запишем $x=dx_1$, $z=dz_1$, где $d=\gcd{(x,z)}$. Тогда $d^2x_1^5+x_1^2z_1-z_1^3=0$. Отсюда $z_1^3$ делится на $x_1$ и, таким образом, $x_1=\pm 1$. Далее получим уравнение $d^2=u^3-u$, где $u=\pm z_1$. Легко видеть, что оно имеет только тривиальные (где $d=0$) решения в целых числах.

Старинный сюжет, на который я намекал в стартовом сообщении --- это о решении уравнения $d^2=u^3-u$ в рациональных числах (уравнение $x^5+x^2z-z^3=0$ к нему сводится подстановкой $x=d$, $z=du$). Здесь тоже есть только тривиальные решения. Это утверждение эквивалентно ВТФ для показателя $4$.

[Markiyan Hirnyk]

Все это механизировано ы Математике и других СКА..

AsymptoticSolve[x^5 + x^2*y^2 == y^6, y, {x, 0, 4}]

\left\{\left\{y\to -i x^{3/2}\right\},\left\{y\to i x^{3/2}\right\},\left\{y\to -\frac{x^{5/2}}{4}-\sqrt{x}\right\},\left\{y\to \frac{1}{4} i x^{5/2}-i \sqrt{x}\right\},\left\{y\to i \sqrt{x}-\frac{1}{4} i x^{5/2}\right\},\left\{y\to \frac{x^{5/2}}{4}+\sqrt{x}\right\}\right\}