Вообще, если честно и полностью обсчитать весь рабочий участок:
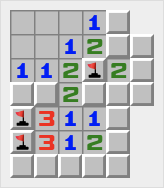
То получится следующее. Размер участка и области вне его:


Внутри участка возможно 20 вариантов размещения не отмеченных мин:
- 6 случаев с 5-ю минами

"Комбинационный вес" каждого этого случая 
- 14 случаев с 6-ю минами

"Комбинационный вес" каждого этого случая 
Здесь

Полный "комбинационный вес" всех этих случаев

Шанс нарваться на мину в нижнем левом углу (под нижним флажком, а так же под нижней двойкой) будет значительно больше 1/3:

Шанс нарваться на мину под нижней тройкой будет чуть по-меньше:

Шанс нарваться на мину под нижней единицей минимальный из этих трёх взаимоисключающих событий:

Шанс нарваться на мину в одной из трёх ячеек самого правого столбца рабочего участка, пожалуй, самый маленький из того, что есть:

Шанс нарваться на мину над самой правой двойкой:

Шанс нарваться на мину под самой правой двойкой:

Шанс нарваться на мину слева от этой ячейки (по верхним флажком) такой же.
Шанс нарваться на мину вне рабочего участка:
 Надеюсь, нигде не обсчитался и не пропустил никаких вариантов размещения мин.
Надеюсь, нигде не обсчитался и не пропустил никаких вариантов размещения мин. Таки пропустил варианты. Надеюсь теперь всё на месте.
-- 06.09.2024, 16:58 --RobinGood, вы двигались в правильном направлении, но не учли всю имеющуюся информацию. Цепочка связей через двойку, а потом через единицу портит вам весь расчёт.