Тогда другая задача на обращение Мебиуса. Определить сходимость ряда:

где

- мнимая единица а

- постоянная, в случаях:
1.

.
2.

?
Общее:
1)

мультипликативна, если

удовлетворяет

для

. Значит и общий член ряда мультипликативен.
2) Как уже было сказано, для всякой мультипликативной арифметической функции

выполнено

3) При

имеем

3.2) Для

это

, а для
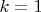
это

. Тогда ряд равен произведению вида

, которое сходится.
3.1) Имеем

. Поделив выражение из 3) на

, получим

.
Тогда произведение сходится т.т.т сходится сумма

(логарифмируем произведение и отбрасываем слагаемые порядка малости

. Такая сумма должна расходиться, наверное.