6+10 6+11 6+12 5+11 5+12
b319 b392 b467 b74 b65
-p50 -x1e27 0.6 0.6 0.6 2.1 2.1
-p50 -x1e28 0.8 0.9 0.8 19 19
-p50 -x1e29 2.2 2.3 2.1 182 183
-p50 -x1e30 16 17 15 . .
-p50 -x1e31 147 150 147 . .
-p100 -x1e27 19 19 19 17 17
-p100 -x1e28 51 49 51 91 86
-p100 -x1e29 98 100 97 767 .
-p100 -x1e30 232 238 230 . .
-p100 -x1e31 1243 . . . .
-p150 -x1e27 78 76 77 65 63
-p150 -x1e28 194 188 186 192 193
-p150 -x1e29 482 . . 1213 .
-p200 -x1e27 180 . . 142 .
-p300 -x1e27 365 . . 272 .
-p400 -x1e27 558 . . 413 .
-p500 -x1e27 767 . . 563 .
-p700 -x1e27 1200 . . 870 .
-p1000 -x1e27 1770 . . 1270 .

 , first to see how often additional chains appear above the smallest, and second to see how the maximum squared prime is distributed across them.
, first to see how often additional chains appear above the smallest, and second to see how the maximum squared prime is distributed across them. . I would suggest experimenting with something very fast like
. I would suggest experimenting with something very fast like  to work out a methodology, then using full runs of
to work out a methodology, then using full runs of  to get more realistic data.
to get more realistic data. , a run up to
, a run up to  finds 306 distinct solutions. Grouped by powers of 2, they distribute as
finds 306 distinct solutions. Grouped by powers of 2, they distribute as  where the first number implies 3 solutions in the range
where the first number implies 3 solutions in the range  . I get that (in 170s) using:
. I get that (in 170s) using: (исходники не смотрел), товарищ пытается единым махом перекрыть все возможные низины, рекурсивно получая все возможные паттерны и выходя по каждому из них на примерно нашу же проверку (только не по isprime, а сразу по numdiv). Насколько корректно (перекрывая все возможности и строго по возрастанию чисел) генерятся паттерны я не смотрел.
(исходники не смотрел), товарищ пытается единым махом перекрыть все возможные низины, рекурсивно получая все возможные паттерны и выходя по каждому из них на примерно нашу же проверку (только не по isprime, а сразу по numdiv). Насколько корректно (перекрывая все возможности и строго по возрастанию чисел) генерятся паттерны я не смотрел. , пока выгодно, но стоит увеличить любое простое вдесятеро (или все в полтора раза) и всё, выгода исчезает. И выходит выгоднее сразу исключить перебор 6-го простого, 6.2млрд итераций ускоритель выполнит секунд за 5-10, перебор же 6-го простого в квадрате будет где-то до 1e10-1e12, что намного дольше. И с увеличением первых 5-ти простых ускоритель будет выполняться быстрее, а квадратичный перебор нет.
, пока выгодно, но стоит увеличить любое простое вдесятеро (или все в полтора раза) и всё, выгода исчезает. И выходит выгоднее сразу исключить перебор 6-го простого, 6.2млрд итераций ускоритель выполнит секунд за 5-10, перебор же 6-го простого в квадрате будет где-то до 1e10-1e12, что намного дольше. И с увеличением первых 5-ти простых ускоритель будет выполняться быстрее, а квадратичный перебор нет. , иначе или
, иначе или 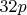 не даёт
не даёт  , или
, или  не даёт
не даёт  не влезает в цепочку:
не влезает в цепочку: нельзя получить ни с каким
нельзя получить ни с каким  если перед ним будет коэффициент 10,21,22,27:
если перед ним будет коэффициент 10,21,22,27: больше 22 и меньше 144 я запретил для цепочек длиной 12+ на 140-й странице темы.
больше 22 и меньше 144 я запретил для цепочек длиной 12+ на 140-й странице темы. может быть только на 32p-3, но тогда на 32p+2 будет
может быть только на 32p-3, но тогда на 32p+2 будет  , что запрещено, так что
, что запрещено, так что  может быть только на 32p-1, но тогда на 32p+6 будет
может быть только на 32p-1, но тогда на 32p+6 будет  , что запрещено, значит цепочек длиной 14+ с
, что запрещено, значит цепочек длиной 14+ с  ?
? , а надо было ещё на 3 умножить:
, а надо было ещё на 3 умножить:  . Логично, молодцы.
. Логично, молодцы.  и
и  я исключил давно. Этих кубов ведь даже нет в моём списке проверяемых модулей, хотя другие кубы есть:
я исключил давно. Этих кубов ведь даже нет в моём списке проверяемых модулей, хотя другие кубы есть: . Сложнее всего запретить
. Сложнее всего запретить  , там семёрку некуда поставить.
, там семёрку некуда поставить. , но и вокруг
, но и вокруг  .
. всё время справа от
всё время справа от  и
и  пока вполне подходят.
пока вполне подходят. — 1163 (1044);
— 1163 (1044); — 578 (504);
— 578 (504); — 3704 (3408);
— 3704 (3408); — 1116 (1044);
— 1116 (1044); — 528 (488).
— 528 (488). встречаются исключительно вместе. Т.е. в цепочках длиной 14+ они присутствуют все, а в цепочках длиной 13 квадрата
встречаются исключительно вместе. Т.е. в цепочках длиной 14+ они присутствуют все, а в цепочках длиной 13 квадрата