пианист(Оффтоп)
Вначале рассмотрим функцию
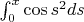
. Заменим переменную:
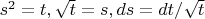
. Итого эта функция преобразуется преобразуется в
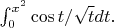
. Теперь надо оценить скорость сходимости нового интеграла, помня про верхний предел

, а пока рассматриваем интегралы
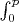
и
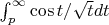
. Проинтегрируем по частям:
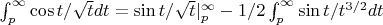
. Для последнего интеграла опять придется оценивать: аналогично,
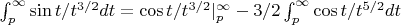
. Последний интеграл с косинусом уже оценим руками, т.к. он убывает быстро: можно оценить сверху как интеграл от степенной
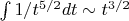
.Таким образом видно, что функция
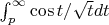
оценивается как
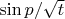
плюс члены порядка не ниже
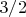
. Теперь вспомним, что
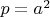
на самом деле, а значит, имеем оценку
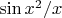
.
Только ощущение, что где-то двойку потерял (а может не потерял?) - да,
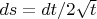
, разумеется., значит, оценка будет
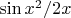
.