10.0e9<=p<=35.4e9, 8<=qr<=100, #qr=31
57*12201437869^2:8485879906050833886169: 16, 32, 32, 12, 12, 12, 12, 12, 12, 12, 4, 48, 8,128, 12, valids=8, maxlen=7
57*12290384531^2:8610052459431113127769: 8,128, 16, 48, 12, 12, 12, 12, 12, 12, 32,192, 16, 32, 24, valids=6, maxlen=6
34*14583426017^2:7230994689372624465817: 8, 4, 16,384, 16, 12, 12, 12, 12, 12, 12, 96, 4, 16, 32, valids=6, maxlen=6
15*17360956999^2:4521042418816906290009: 24, 32, 16, 24, 2, 12, 12, 12, 12, 12, 12, 48,192,256, 4, valids=6, maxlen=6
15*20009954297^2:6005974064520431463129: 16, 32, 4,384, 12, 12, 12, 12, 12, 12, 2, 96, 16, 16, 16, valids=6, maxlen=6
15*25266482119^2:9575926780046200952409: 96, 32, 4, 48, 12, 12, 12, 12, 12, 12, 8,192, 32, 16, 2, valids=6, maxlen=6
14*26702310779^2:9982187613136194215769: 32, 32, 8, 24, 64, 12, 12, 12, 12, 12, 8, 48, 16, 16, 32, valids=5, maxlen=5
6.0e9<=p<=10.0e9, 8<=qr<=278, #qr=84
34*8338771633^2:2364193819809066547417: 4, 32, 32, 24, 12, 12, 12, 12, 12, 12, 32,192, 2, 32, 96, valids=6, maxlen=6
34*9749714783^2:3231935903894857061017: 4, 32, 16, 48, 12, 12, 12, 12, 12, 12, 32, 96, 4, 16, 16, valids=6, maxlen=6
4.0e9<=p<=6.0e9, 8<=qr<=623, #qr=184
15*4494282983^2:302978692969250674329: 12, 16, 4,192, 12, 12, 12, 12, 12, 12, 8, 48, 32, 32,128, valids=7, maxlen=6
57*4561046131^2:1185779083119273942169: 8, 64, 64, 96, 12, 12, 12, 12, 12, 12, 4, 96, 4, 32, 80, valids=6, maxlen=6
...

 ? 99% что никто. Ну и зафига тогда городить огород?!
? 99% что никто. Ну и зафига тогда городить огород?! 
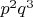 ):
): уменьшен до 10e9.
уменьшен до 10e9. , so I wrote my own version of this code (at
, so I wrote my own version of this code (at 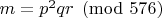 at the very start, and continue testing only if
at the very start, and continue testing only if 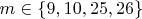 . That is enough to verify that the
. That is enough to verify that the 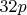 is not divisible by 2 or 3, and that
is not divisible by 2 or 3, and that 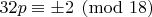 . (I'm fairly sure I have the right values for
. (I'm fairly sure I have the right values for  , after stepping through a handful of cases.)
, after stepping through a handful of cases.)