Мы поспорили с
Doctor Boom на тему, удовлетворительно ли Колмогоров аксиоматизировал теорию вероятностей. Поскольку я не претендую на звание глубокого знатока теории вероятностей, пусть уважаемые математики рассудят, кто из нас прав.
ЛС, на которые я здесь отвечаю, цитируются с согласия автора. Также по согласованию с модератором цитирую кое-что из Пургатория.
Doctor Boom писал(а):
Ну вот вам мнения других математиков

Цитата:
Некоторые учёные не согласны с тем, что Колмогоров сделал теорию вероятностей аксиоматической теорией. Их доводы:
Вероятность — это понятие реального мира, поэтому её невозможно аксиоматизировать, можно только построить математическую модель. Например, так же невозможно аксиоматизировать понятие «мост», что не мешает рассчитывать мосты на прочность, строя математические модели, со свойствами похожими на настоящие мосты.
Мой ответ. Дело математики и есть строить математические модели, а не изучать настоящие мосты из железобетона. И пока и поскольку мы считаем теорию вероятностей разделом математики, аксиоматика Колмогорова исчерпывающе отвечает нам на вопрос, что такое вероятность.
Для моделирования с.в. с любым распределением вам нужна с.в. с равномерным распределением, ее вы получаете из реального мира - алгоритмы псевдоГСЧ, тепловой шум, квантовые коллапсы, ее нельзя получить из каких-то там мер.
Ну, для начала, какой Вам алгоритм псевдоГСЧ "реальный мир"? ПсевдоГСЧ потому и псевдо-, что это алгоритм, каждая выдача которого предопределена в том же смысле, в каком предопределены все знаки числа

. Это же математическая абстракция в чистом виде.
И потом, задача высосать случайную величину из пальца зачастую и не стоит. Стоит задача, например, определить погрешность измерения по множеству отдельных измеренных значений. Или там вывести закон распределения доходов населения. Не должен же я рассказывать про задачи математической статистики, правда?
А еще есть, например, целый раздел электродинамики, без которой приличный радиоастроном или ионосферщик сразу повесился бы: распространение волн в случайно-неоднородных средах. Заметьте, в случайно-неоднородных, а не в случайно-нестационарных. Неоднородности не появляются друг за другом во времени, как при работе ГСЧ или тепловом шуме. Они к началу распространения волны даны нам все сразу, налицо. Просто их очень много, в них нет никакой простой закономерности, и лучший способ их описать и учесть - случайная величина. А будь это не офигиллиард неоднородностей на пути радиоволны, а несколько ям на дороге с работы домой? Тогда эффективнее было бы просто запомнить их все, чтобы водитель точно знал, где какую объехать. И тут величина - бац - перестала быть случайной! Без регистрации, sms и упразднения квантовых коллапсов.
Или другой пример. Палеонтологи применяют байесовы методы, чтобы решить, к какому виду и роду относился динозавр, чьи полторы кости они нашли. Это применение теории вероятностей? Конечно! Только вот они не знают, что их разыграл злобный доктор Экс, который стащил эти полторы кости из полного скелета курозавра пупырчатого. Он-то точно знает и род, и вид. Есть для него какая-то вероятность или случайность в видовой принадлежности сей рептилии? Вряд ли. И не потому, что для шутника и его коллег природа разная. А потому, что он знает, а они нет.
Несколько огрубляя ситуацию, можно сказать, что
мы считаем величину случайной и применяем к ней аппарат теорвера, когда не знаем и не пытаемся узнать, какое в точности значение она примет. Почему не знаем - дело десятое. Может быть, потому что это тепловой шум или выдача генератора псевдослучайных чисел. А может быть, потому что мы не измерили заранее рост всех тех людей, которым мы собираемся продавать штаны. Не вызубрили назубок координаты каждой звезды, видимой на небе невооруженным глазом. А это с хорошей точностью пуассоново распределение за пределами видимой полосы Млечного Пути - как Вам Галактика в роли генератора случайных чисел? Или не держали свечку 70 миллионов лет назад, когда курозавр пупырчатый окучивал свою курозавриху. Но как минимум в некоторых из этих случаев мы
могли бы заранее иметь точную информацию и не считать величину случайной. Никакой "случайности, объективно существующей в природе", не требуется.
Doctor Boom писал(а):
И как вы из экспоненты собрались сделать черный ящик? Мне прям интересно, а мы уже не в Прр

Вот так. Позвольте только не из экспоненты, а их

, чтобы нигде не менять

на

.
Для начала дадим общее определение. Рассмотрим пространство

с заданной на нем сигма-алгеброй

. Рассмотрим также вероятностное пространство

.
Случайной величиной

называется

-измеримая функция
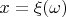
, определенная на

и принимающая значения из

.
Как это соотносится с клише "случайная величина принимает значение в результате опыта"? На этом языке можно сказать следующее. Когда в результате опыта появляется тот или иной элементарный исход

, случайная величина

принимает значение

, однозначно определённое этим элементарным исходом:
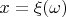
. Мы можем говорить о вероятности того, что

примет значения из некоторого подмножества

, и все имеющие вероятность подмножества

образуют сигма-алгебру

. Вероятность того, что

примет значение из

, есть вероятность события

(которое по условию

-измеримости функции

таки событие, т.е. принадлежит

и, следовательно, имеет вероятность).
Теперь пусть

,

- борелевская сигма-алгебра над

. Нужно еще задать на

вероятностную меру. С этим справится любая функция, удовлетворяющая требованиям к интегральному закону распределения, например, нормальный закон. Это, кстати, будет закон распределения случайной величины
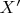
, заданной функцией

. Эта не та СВ, которую мы строим, но нам сейчас важно превратить

в вероятностное пространство. Теперь осталось положить, что

. Полином - борелевская функция, так что требование измеримости выполнено. Фсё.
Теперь то же на языке опыта. Каждый раз, когда в результате опыта появляется тот или иной элементарный исход

, случайная величина

принимает значение

. Для любого борелевского множества

определена вероятность того, что

.
Предвижу возражение: "Аааа, в результате оооопыыыта? У вас там в конструкции все равно спрятался мальчик, который бьет палкой по черному ящику! А вот вы напишите компьютерную программу, чтобы она из этого вашего

чеканила числа, которые лично я сочту случайными!". Как я уже говорил в самом начале, это возражение класса "почему по математической модели моста нельзя перейти реку". Но, может быть, я не прав и чего-то не понимаю.
А, уважаемые математики?