Докажем по индукции следущее утверждение: квадрат любого взаимнопростого с 10 натурального числа

, для которого

является квадратичным вычетом, представим в виде

с взаимнопростыми

и

. Базой индукции являются все числа меньшие 5, из которых по условию подходит только 3.

. Теперь индукционный переход. Поскольку

квадратичный вычет по модулю

, то найдутся целые числа

и

, такие что

.

выберем так, что оно чётное и

. Тогда

. Возможны два случая:

либо делится на 5, либо не делится. Рассмотрим первый случай (второй рассматривается аналогично). Возведём равенство

в квадрат и получим

. Если
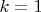
, то утверждение доказано. Пусть

- простой делитель

и

. Тогда

. Поскольку

, то для

верно предположение индукции и оно представимо в виде

с взаимнопростыми

и

. Но тогда по лемме из стартового сообщения получаем, что

также представимо в таком виде. Пусть

. Если

, то будем повторять ту же процедуру с выделением простого делителя до тех пор пока не получим

и

.
В общем случае (утверждение 4 из моего предыдущего сообщения), для формы

можно дать похожее доказательство, но нужно предварительно доказать следущую лемму: Если нечётное натуральное число

представимо в виде

с взаимнопростыми

и

, то для любого натурального

:

также представимо в виде

с взаимнопростыми

и

.
Дополнение о том, как получить критерий представимости натурального числа в виде

.
Лемма. Пусть

- нечётное натуральное число взаимнопростое с 10.

представимо в виде

с взаимнопростыми

и

тогда и только тогда, когда хотя бы одно из чисел

и

представимо в виде

с взаимнопростыми

и

.
Доказательство. Если

, то

. Если

, то

. Если

, то

.

и

либо взаимнопросты, либо их НОД равен 2. В первом случае среди этих чисел один квадрат и один упятерённый квадрат, а их сумма

представима в виде

. Во втором случае аналогично получается, что

представимо в виде

.
Как определить, когда

, а когда

? Это можно сделать, рассмотрев эти равенства по модулю 5. Ровно одно из них будет разрешимо. Например, если

, то

, а первое равенство невозможно по модулю 5.