Есть и более простое рассуждение, которое годится, например для

Существует
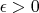
т.ч. каждом

существует подинтервал длины
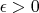
на котором подынтегральное выражение

. С другой стороны, подынтегральное выражение неотрицательно, поэтому

,

, и расходимость интеграла следует из расходимости ряда

.