формулы получены верно (проверил в ВольфрамАльфа)
Вывод о существовании производной при
неверный. Производной там нет (производная терпит разрыв)
В точках

ведь даже производная

не существует.
И ещё, Вы пишете

, а правильное обозначение

.
Но ведь производная
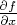
существует. И предел,
![\[ \lim_{y \to 0} { { |y| \over x^2 + y^2} - 0 \over y - 0} = 0 \] \[ \lim_{y \to 0} { { |y| \over x^2 + y^2} - 0 \over y - 0} = 0 \]](https://dxdy-01.korotkov.co.uk/f/0/e/8/0e8eab12de9ad50029caf3efe835392b82.png)
Значит, существует и смешанная производная

, разве не так?
P.S. Доказательство существования предела:
![\[ \lim_{y \to 0} { { |y| \over x^2 + y^2} - 0 \over y - 0} = \lim_{y \to 0} {|y|y \over x^2 + y^2} = \lim_{y \to 0} {sign(y) y^2 \over x^2 + y^2}. \] \[ \lim_{y \to 0} { { |y| \over x^2 + y^2} - 0 \over y - 0} = \lim_{y \to 0} {|y|y \over x^2 + y^2} = \lim_{y \to 0} {sign(y) y^2 \over x^2 + y^2}. \]](https://dxdy-03.korotkov.co.uk/f/e/0/3/e03e3ac1b26cae2709c1c5b60951f38282.png)
Рассмотрим левосторонний и правосторонний пределы:
![\[ \lim_{y \to +0} {sign(y) y^2 \over x^2 + y^2} = \lim_{y \to +0} {y^2 \over x^2 + y^2}. \] \[ \lim_{y \to +0} {sign(y) y^2 \over x^2 + y^2} = \lim_{y \to +0} {y^2 \over x^2 + y^2}. \]](https://dxdy-03.korotkov.co.uk/f/e/5/e/e5e69709389d9110c176ac38603110d382.png)
Числитель этой дроби стремится к 0, знаменатель этой дроби стремится к

,

по условию. Тогда, вся дробь стремится к 0.
![\[ \lim_{y \to -0} {sign(y) y^2 \over x^2 + y^2} = \lim_{y \to -0} {-y^2 \over x^2 + y^2}. \] \[ \lim_{y \to -0} {sign(y) y^2 \over x^2 + y^2} = \lim_{y \to -0} {-y^2 \over x^2 + y^2}. \]](https://dxdy-01.korotkov.co.uk/f/0/a/5/0a58a2c916610c375d7607e040745c0b82.png)
Числитель этой дроби стремится к 0, знаменатель этой дроби стремится к

,

по условию. Тогда, вся дробь стремится к 0.
Левосторонний и правосторонний пределы равны, значит, предел существует и равен 0.