SomeoneТак доказать

можно только если предположить

и вывести из этого противоречие
Извините, это какая-то ерунда (не обижайтесь). Особенно если учесть, что в классической логике любая формула может быть записана в виде
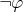
.
можно сначала диагональным методом доказать

, но после этого всё равно придётся предполагать счётность и выводить противоречие, чтобы вывести

Зачем делать такое предположение, если мы уже доказали, что никакое отображение

не является биекцией?
У Вас неправильное представление о доказательствах "от противного". Если следовать вашей логике, то все доказательства являются доказательствами "от противного".
На самом деле доказательство "от противного" имеет место только в том случае, когда сделанное предположение необходимо для построения противоречия. Например, в доказательстве иррациональности числа

делается противоположное предположение, что это число рационально, то есть, может быть записано в виде дроби

, где

и

— натуральные числа; если дробь сократимая, её сокращаем на наибольший общий делитель

и

, чтобы дробь стала несократимой, после чего выясняется, что полученная после сокращения дробь сократима на

(в этом и состоит противоречие). Здесь предположение о рациональности

существенно используется в построении противоречия.
В доказательстве теоремы Кантора предположение о равномощности множеств

и

никак не используется. Мы сначала замечаем, что

, так как существует очевидная инъекция

, а затем показываем, что никакое отображение

не является сюръекцией (и тем более не является биекцией), поэтому

. Никаких предположений об отображении

делать не нужно, рассуждение работает для любого отображения. В частности, не требуется предполагать, что

— биекция. Поэтому доказательства "от противного" здесь нет.