Вектора и матрицы

[melnikoff]

Здравствуйте!
Прошу помочь разобраться со следующим моментом.
Смотрю лекции по "Алгебре и геометрии".
В первых двух лекциях лектор дал понятие матрицы, определил операции над ними и вывел их свойства.
Затем, в четвертой лекции (базисы и декартовы СК) доказывается след. утверждение:
Пусть $\mathfrak{e}$ – базис в $V_i (i=1,2,3)$ и вектор $\vec{u}$ имеет в данном базисе координаты $\alpha$, а вектор $\vec{v}$ имеет координаты $\beta$.
Тогда
1. Вектор $\vec{u}+\vec{v}$ имеет координаты $\alpha+\beta$.
2. Вектор $\lambda\vec{u}$ имеет координаты $\lambda\alpha.
Доказательство:
1. $\vec{u}+\vec{v} = \mathfrak{e}\alpha + \mathfrak{e}\beta =$ в силу левой дистрибутивности умножения матриц (почему?!) $=\mathfrak{e}(\alpha+\beta)$. Чтд.
Сразу возникает вопрос: На каком основании мы тут можем апеллировать к свойствам матриц? Мы же операции над матрицами определяли до этого независимо от векторов.
2. $\lambda\vec{u}=\lambda(\mathfrak{e}\alpha) = $ в силу ассоциативности умножения матриц и коммутативности умножения матрицы на скаляр (почему?!)$=\mathfrak{e}\lambda\alpha$. Чтд.
Аналогичный вопрос. Почему мы можем тут использовать свойства матриц, если запись $\mathfrak{e}\alpha$ мы тут используем просто в целях компактности, используя определение операции умножения матриц (тут строки на столбец).

[Sinoid]

melnikoff в сообщении #1518154 писал(а):

Мы же операции над матрицами определяли до этого независимо от векторов.

Даже если и так (хотя обычно наоборот). Так правильно. И теперь мы операции над векторами сводим к операциям над матрицами.

[arseniiv]

melnikoff в сообщении #1518154 писал(а):

Почему мы можем тут использовать свойства матриц, если запись $\mathfrak{e}\alpha$ мы тут используем просто в целях компактности, используя определение операции умножения матриц (тут строки на столбец).

Если введены только матрицы над числами, то не можем, это так. То есть мы можем рукомахательно понадеяться, что используем аналогию, доводимую до чего-то корректного, но это конечно уже не тот же уровень строгости.

Но не является ли там $\mathfrak{e}$ матрицей? Естественно понимать как матрицу, если все векторы, которые у нас определены — столбцы чисел (но вы эту деталь не описали, а смотреть видео мне лично лень ) — тогда базис, как строка таких столбцов, и будет матрицей. (Определять все векторы исключительно как столбцы чисел нехорошо, но это другая история.)

[Sinoid]

arseniiv в сообщении #1518183 писал(а):

Но не является ли там $\mathfrak{e}$ матрицей?

Скорее всего, так и есть. Столбец.

-- 11.05.2021, 22:43 --

(Оффтоп)

arseniiv в сообщении #1518183 писал(а):

а смотреть видео мне лично лень

В том числе вот по какой причине я предпочитаю новый материал изучать по книгам, а не по видео.

[arseniiv]

Sinoid в сообщении #1518187 писал(а):

Скорее всего, так и есть. Столбец.

Не, ТС говорит, что это как минимум строка базисных векторов, а координаты образуют столбец. Тогда я надеялся, что $\mathfrak{e}$ могло бы быть квадратной матрицей из чисел, а не просто строкой. Матрица-строка из векторов — действительно вещь ещё та, и строго говоря без какой-нибудь жутко общей линейной алгебры мы такими объектами оперировать не должны, а то это будет искусство, и кто-то может не напортачит, а кто-то зато выведет $1 = 0$. То есть мы можем ввести эмпирические правила «матрица из векторов может умножаться только на матрицу из чисел, если у нас нет скалярного произведения» и т. п., но так же изучающие только больше запутаются.

[svv]

Откройте третью лекцию, 1:13:44. В левой части доски записано разложение вектора $\vec u$ по базисным векторам $\vec e_i$:
$\vec u=\sum\alpha_i\vec e_i=\mathfrak{e}\cdot \alpha\,,$
где последнее — просто краткое обозначение для суммы.

[melnikoff]

svv в сообщении #1518190 писал(а):

Откройте третью лекцию, 1:13:44. В левой части доски записано разложение вектора $\vec u$ по базисным векторам $\vec e_i$:
$\vec u=\sum\alpha_i\vec e_i=\mathfrak{e}\cdot \alpha\,,$
где последнее — просто краткое обозначение для суммы.

Я именно об этом и говорю. Мы используем $\mathfrak{e}\cdot \alpha$ для сокращения суммы, а потом, внезапно, начинаем апеллировать к свойствам матриц.

[svv]

А, теперь я Вас понял. Может быть, преподаватель опирался на то, что возможна запись разложения вектора по базису в виде такого символического произведения, где элементами первого вектора(-строки) являются базисные векторы:
$\mathfrak{e}\cdot \alpha = \begin{bmatrix}\vec{e}_1&\vec{e}_2&\ldots&\vec{e}_n\end{bmatrix} \begin{bmatrix}\alpha_1\\\alpha_2\\\ldots\\\alpha_n\end{bmatrix}$

-- Вт май 11, 2021 21:15:23 --

О том же упоминал arseniiv.

[artempalkin]

melnikoff в сообщении #1518192 писал(а):

Я именно об этом и говорю. Мы используем $\mathfrak{e}\cdot \alpha$ для сокращения суммы, а потом, внезапно, начинаем апеллировать к свойствам матриц.

Да, меня всегда тоже этот момент смущал.

Но, строго говоря, свойства произведения матриц выводятся (что может быть очевиднее) из правил, по которым матрицы перемножаются, правильно? Поэтому если наше "символическое" умножение строки, составленной из элементов ЛП (то есть, как говорят, "элементов произвольной природы", а не столбцов или чисел) на реальный числовой столбец происходит по таким же правилам, то и все свойства умножения "матриц", составленных из подобных элементов, тоже можно вывести и дальше ими пользоваться.

На месте лекторов я, конечно, этот момент прояснял бы. Человек, который пытается понять линал глубоко, рано или поздно тут споткнется :) Хотя как споткнется, так и разберется.

[melnikoff]

artempalkin, идея в целом ясна. Попробую это зафиксировать.

В алгебре матриц (1-2 лекции), свойство левой дистрибутивности умножения матриц (а для доказательства п.1 нам нужна именно она) доказывалось после введения двух операций: умножения матриц и сложения матриц.
И делалось это так:
Пусть $A\in M_{m\times n}(\mathbb{R})$ и $B, C\in M_{n\times k}(\mathbb{R})$. Тогда
$A\cdot (B+C) = \sum\limits_{s=1}^{n}[A]_{is}[B+C]_{sj} = \sum\limits_{s=1}^{n}[A]_{is}([B]_{sj}+[C]_{sj}) =\\ =\sum\limits_{s=1}^{n}([A]_{is}[B]_{sj}+[A]_{is}[C]_{sj}) =\sum\limits_{s=1}^{n}[A]_{is}[B]_{sj} +\sum\limits_{s=1}^{n}[A]_{is}[C]_{sj} = A\cdot B + A\cdot C.$
То есть для доказательства левой дистрибутивности умножения матриц c элементами из $\mathbb{R}$ нам понадобилось два определения (умножение матриц и сложение матриц) и три аксиомы поля $\mathbb{R}$ (дистрибутивность умножения относительно сложения, ассоциативность сложения и коммутативность сложения).

Теперь вернемся к утверждению из п.1:
Пусть $\mathfrak{e}$ – базис в $V_i (i=1,2,3)$ и вектор $\vec{u}$ имеет в данном базисе координаты $\alpha$, а вектор $\vec{v}$ имеет координаты $\beta$.
Тогда
1. Вектор $\vec{u}+\vec{v}$ имеет координаты $\alpha+\beta$.
Доказательство:
$\vec{u}+\vec{v} = \sum\limits_{i=1}^n\alpha_i\vec e_i + \sum\limits_{i=1}^n\beta_i\vec e_i$
Определим данные суммы как произведение строки базисных векторов на столбец координат данного вектора: $\vec u=\sum\limits_{i=1}^n\alpha_i\vec e_i=\mathfrak{e}\cdot \alpha$ и $\vec v=\sum\limits_{i=1}^n\beta_i\vec e_i=\mathfrak{e}\cdot \beta$.
Кроме этого мы ещё должны определить сложение координат-столбцов таким образом, чтобы $\sum\limits_{i=1}^n\alpha_i\vec e_i + \sum\limits_{i=1}^n\beta_i\vec e_i = \sum\limits_{i=1}^n(\alpha+\beta)_i \vec e_i$.

И уже, исходя из этих определений (а не из свойств вещественных матриц !), мы можем записать
$\mathfrak{e}(\alpha+\beta) = \sum\limits_{i=1}^n \vec e_i(\alpha+\beta)_i = \sum\limits_{i=1}^n \vec e_i(\alpha_i+\beta_i) = \sum\limits_{i=1}^n (\vec e_i\alpha_i+\vec e_i\beta_i) = \\ =\sum\limits_{i=1}^n \vec e_i\alpha_i + \sum\limits_{i=1}^n \vec e_i\beta_i = \mathfrak{e}\alpha$ + \mathfrak{e}\beta,
что доказывает исходное утверждение.
Я правильно понял?

[artempalkin]

melnikoff в сообщении #1518376 писал(а):

Я правильно понял?

Ага

melnikoff в сообщении #1518376 писал(а):

что доказывает исходное утверждение.

Да, доказывает, и к тому же позволяет нам пользоваться таким формализмом в дальнейшем.
Не знаю, дошли ли вы до этого уже, там дальше матрица перехода определяется как $\mathfrak{e}C=\mathfrak{f}$. Тут действует тот же принцип (и тоже не припомню, чтобы я встречал пояснения на эту тему в учебниках).

Еще хитрее вот такая запись, раскрутить которую у меня никогда не доходили руки (и сейчас неохота, если честно), хотя в некоторых доказательствах на моей памяти она бы сильно упростила записи: $\mathfrak{e}^T\mathfrak{e}=G(\mathfrak{e})$, где $G$ - матрица Грама.

[arseniiv]

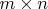
Вообще так же как матрицы $m \times n$ из скаляров $K$ логично отождествлять с линейными отображениями $K^n \to K^m$, матрицы-строки дадут отображения $K^n \to K$, аналогично матрицы-строки из векторов $V$ — это линейные отображения $K^n \to V$, а вот чтобы адекватно формализовать матрицы-столбцы из ковекторов $V^*$, придётся сначала разделить пространства столбцов $K^n$ и пространства строк ${}^n K$. У нас есть естественное билинейное ${}^n K \times K^n \to K$, так что мы отождествим ${}^n K \equiv (K^n)^*$ и наоборот. Матрицы-столбцы из $V^*$ получатся линейными отображениями ${}^n K \to V^*$. Сопряжённым отображением будет $V \to K^n$, и вот это мы можем нормально умножить на матрицу-строку $K^n \to V$ и получить квадратную матрицу $K^n \to K^n$.

При формализации матриц я бы правда лучше сразу перешёл к тензорным произведениям пространств. Тогда матрица-столбец из ковекторов — это $K^n \otimes V^*$, матрица-строка из векторов — ${}^n K \otimes V$, берём их тензорное произведение, берём след, остаётся $K^n \otimes {}^n K$.

Но вообще матрица Грама — это ведь матрица билинейной формы, чего с ней мудрить? Ради матриц перехода и общего рассмотрения линейных отображений между разными пространствами логично ввести матрицы отображений — и операторов — в двух базисах, исходном и конечном, а для матрицы Грама, чтобы она не оказывалась неудобно выглядящей строкой строк, логично понимать её как матрицу отождествления $V \to V^*$ (или наоборот), где один базис обычный на $V$, а второй двойственный к нему (но не через скалярное произведение — а то получится всегда диагональная каноническая матрица формы). Матрицы отображений, взятых в разных базисах разных пространств, нужно просто умножать только на подходящие матрицы, а в остальном ничего нового. Матрицы из сложенных друг на друга векторов тоже работают через $K^n$ как выше, но понадобятся нам в меньшем числе случаев: ни для матриц перехода, ни для матрицы Грама в принципе не будут нужны.