Штуки называются "разностные методы", найти можно много где. Попробуйте начать с работ А.А. Самарского
Спасибо, про разностные методы на сетках с постоянным шагом, когда
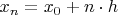
, я знаю, и даже постоянно пользуюсь. Вроде существуют адаптивные сеточные методы, но там вроде просто шаг сетки, где нужно, уменьшается.
Меня же интересует случай, когда расстояния между точками может быть произвольным:

распределены как-то произвольно на неком интервале
И если уж пошла такая пьянка, это всё чтобы могло происходить в многомерном случае.
