"Наличие в комплексном пространстве двух типов линейных функций приводит к существованию целых четырех типов билинейных функций -- линейных первого рода и по

и по
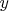
, первого рода по

и второго рода по
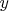
, второго рода по

и первого по
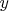
и второго рода по обоим аргументам. Но третий и четвертый типы комплексно сопряжены соответственно ко второму и первому, а билинейные функции первого типа определяются в комплексном пространстве буквально так же, как и в вещественном. Поэтому мы остановимся подробнее лишь на билинейных формах второго типа." (Гельфанд. Лекции по линейной алгебре, стр. 88-89.)
1.
Что имеется в виду под "третий и четвертый типы комплексно сопряжены соответственно ко второму и первому"?
Возьмем второй и третий типы.
Если (по Гельфанду) второй тип это

, то третий тип (который не рассматривается) это

, не так ли?
В таком случае

и

должны быть комплексно сопряжены по отношению друг к другу.
Но это так, только если

есть вещественное число.
То же самое касается первого и четвертого типа.
Если первый тип это
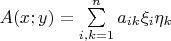
, то четвертый должен быть

.
В таком случае и они также будут комплексно сопряжены по отношению друг к другу, только если

вещественное число.
Имеет ли в виду Гельфанд, что речь идет лишь о формах, матрицы которых вещественны?
2.
Под тем, что "билинейные функции первого типа определяются в комплексном пространстве буквально так же, как и в вещественном", наверное, имеется в виду, что они удовлетворяют одним и тем же аксиомам?