Я так давно читал учебник линейной алгебры, что не могу вспомнить ни одного доказательства такой теоремы:
Пусть  линейно независимы. Тогда для каких угодно
линейно независимы. Тогда для каких угодно  существует линейное отображение
существует линейное отображение  такое, что
такое, что  .
.
которое не привлекало бы построение базиса

или базиса только

и потом до кучи доказательства, что для всякого конечномерного подпространства

существует линейное
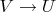
(это даст нам воспользоваться каким-то произвольным отображением из

, чтобы достроить отображение из

до отображения из

).
И вроде тут нигде не должна быть замешана аксиома выбора, или всё-таки замешана?
P. S. Это я решил проверить навык и доказать утверждение из
«Линейная алгебра. Коммутирующие матрицы.» без привлечения матриц. И конечно доказал (и результат удовлетворил), но только вот по модулю требования штучки выше. (Вообще конечно понадобились лишь случаи
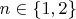
, но общность не повредит; было бы ведь крайне неожиданно, если бы утверждение выполнялось для каких-то

, но не для других.)