Здравствуйте.
Читаю "Линейная Алгебра и геометрия" Шафаревича и Ремизова, на стр. 11 вводится понятие сопряжённых функций.
Пусть

— некоторое фиксированное множество. Обозначим через

совокупность всех отображений

и, аналогично, через

— совокупность всех отображений

. Тогда с каждым отображением

связано определенное отображение

, которое называется сопряженным к

и задается следующим образом. Каждому отображению

оно ставит в соответствие отображение

по формуле:

Формула (5) означает, что для любого элемента

выполнено равенство

, что можно выразить также в виде следующей диаграммы:
![\xymatrix {M \ar[dr]^{f^*(\varphi)} \ar[dd]_{f} & \\ & R \\ N \ar[ur]_{\varphi} &} \xymatrix {M \ar[dr]^{f^*(\varphi)} \ar[dd]_{f} & \\ & R \\ N \ar[ur]_{\varphi} &}](https://dxdy-03.korotkov.co.uk/f/a/4/9/a491b08cd0ccbd95c5987de1eab5e95982.png)
Мы встречаемся здесь с важным общематематическим фактом: функции отображаются в противоположную сторону по сравнению с элементами множеств, на которых они заданы. Это явление проявится и в нашей книге, и позже, в других курсах по отношению к более сложным объектам (например, дифференциальным формам).
И теперь вопрос, что такое эта
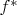
? Судя по рисунку, это отображение M в R, но судя по этому:

, это отображение отображений. Но, во - первых, тогда рисунок не правельный, во - вторых, почему она сопряжённая функции f?
Что такое сопряжённые пространство функционалов я не знаю, что такое преобразование Лежандра не понимаю (надеюсь это узнать и понять из этой книги).