Нелинейная множественная регрессия при нехватке наблюдений

[Lena-Lisa]

Andrey_Kireew в сообщении #1446415 писал(а):

ересь - это отступление от церковных канонов

ЕРЕСЬ — Толковый словарь Ожегова
ЕРЕСЬ Е́РЕСЬ, -и, жен. 1. В христианстве: вероучение, отклонившееся от господствующих религиозных догматов. Впасть в е. 2. перен. Нечто противоречащее общепринятому мнению, пониманию. 3. Нечто ложное, вздор, чепуха (разг.).
Прошу извинить за привнесение в научный разговор лексики из 2-х и 3-х позиций акад. словарей, а не сугубо 1-х. Существует модель полисемии слов русского языка, согласно которой кол-во значений случайно блуждает, т.ч. со временем может остаться одно, и не факт, что это нынешнее первое. У слова даже может оказаться 0 значений, и тогда оно выпадает из языка. Средняя полисемия в русском языке 1,48, т.ч. слово ересь - богатое по значениям.

-- 23.03.2020, 07:58 --

Andrey_Kireew в сообщении #1446415 писал(а):

По сути дела, ответ на Ваш главный вопрос неявно содержится в названии темы - у Вас недостаточно наблюдений для того чтобы использовать нелинейную множественную регрессию.

Еще раз - грубее (не по тону, по сделанным допущениям) уже не бывает.
По глюкозе - из 6 предикторов нетрадицонно повели себя 2 - белок и клетчатка, именно те, которые по функциям отличаются от прочих. Считаем по комбинаторике вероятность случайного выпадения.
По инсулину - нетрадиционен опять белок, что еще уменьшает вероятность случайного выпадения.
Согласитесь, что вероятность выпадения 6 при бросании кости достаточно велика, но двух подряд 6 уже заставляет задуматься, нет ли тут закономерности - не литая ли кость.
А задуматься - значит бросать еще и еще для подкрепления уверенности (или сомнения, как посмотреть). Вопрос был про метод - и баста, и более сведущие, чем я, люди, пришли к мнению, что метод работает. О чем и был вопрос. Всем спасибо за обсуждение, было очень конструктивным.
И, в конце концов, линейная регрессия - частный случай нелинейной, что мешает воспользоваться более общим методом, чтобы потом убедиться, что достаточно было частного? Но меня оно не убедило: при выпадении двух 6 с первого раза, когда это в чью-то пользу, я склонна не считать это случайностью.
Ошибка бывает пропуск цели и ложная тревога, у вас это как-то по другому называется, но смысл ясен. Я более склонна цель не пропускать, так спокойнее живется.

[aitap]

Lena-Lisa, я всё-таки рекомендую хотя бы попытаться оценить разброс значений параметров, с которыми модель описывает имеющийся набор данных, или выполнить любую другую из описанных выше по теме проверок на переобучение. Мы пока не исключили такую потенциально возможную ситуацию, когда другая комбинация тех же 12 параметров описывает данные почти так же хорошо, но предполагает радикально отличающиеся выводы.

[Lena-Lisa]

aitap в сообщении #1446445 писал(а):

я всё-таки рекомендую хотя бы попытаться оценить разброс значений параметров, с которыми модель описывает имеющийся набор данных, или выполнить любую другую из описанных выше по теме проверок на переобучение. Мы пока не исключили такую потенциально возможную ситуацию, когда другая комбинация тех же 12 параметров описывает данные почти так же хорошо, но предполагает радикально отличающиеся выводы.

Но точность подгонки никогда не была критерием истинности именно этой модели.
Вопрос - как искать другие комбинации параметров, если в лоб - по МНК - хорошо бы 120 наблюдений (в 10 раз больше числа прараметров). И все осложняется тем, что данные для каждого наблюдения усреднены всего по 12 испытуемым, и каждое усредненное значение - ср.кв.ош. порядка 5-10-15 при значениях обычно не выше 100 (100=белый хлеб, эталон для шкалы). А точность аппроксимации и по линейной, и по нелинейной моделям также порядка 10-11. Т.ч. исходя из исходных данных, бороться за уточнение нет смысла. А вот из нелинейной модели вытекают вполне опр. следствия:
1. Пей больше воды - будешь на прежнем рационе худеть, поскольку не будет хватать инсулина для утилизации глюкозы. Разве не это проповедуют все вульгарные диетологи, в т.ч. и звездные, исходя из практики (порочной)?
2. Съедай все положенное за 1 прием пищи (вечером) - будешь худеть. Также нехватка инсулина. На практике - диета воина (так питались легионеры Рима в походе).
3. Страдаешь от нехватки инсулина - ешь как можно чаще, инсулина подкалывать придется меньше, или снизить дозу сахаропонижающих.
Т.ч. даже если бы зависимость конструировалась умозрительно, без опоры на экспериментальные данные, для соотвествия 1-3 она оказалась бы схожа с полученной.
Если на основе тех же данных может быть получена иная зависимость, она войдет в противоречие с практикой. Но я не знаю, как ее найти, поискала бы с готовностью, но наверняка по ходу поисков выяснится, что так искать нельзя, и придется вернуться к тому, что и так уже есть.

[Евгений Машеров]

К сожалению, всё, что мы имеем для заданной выборки - точность подгонки. Если есть независимая выборка - хорошо бы проверять по ней, а в качестве протеза контрольной выборки - скользящий экзамен. Но при этом имея в виду, что рост числа параметров модели увеличивает кажущуюся точность, даже если дополнительные параметры никак не осмыслены. А замена 6 параметров на 12 (на каждую переменную не только по коэффициенту перед нет, но и показатель степени) это рост числа параметров и, что существеннее, снижение числа степеней свободы. Кажущаяся ошибка неуклонно снижается, но модель становится вовсе бессмысленной. А то, что не оцениваются одновременно все 12 параметров, а поочерёдно, не отменяет того факта, что подгоняются в итоге все 12. Подобная процедура может быть оправдана облегчением вычислений, или может вместо глобального оптимума привести в локальный и застрять там, но в любом случае это 12 параметров, пусть каждый раз Вы оцениваете не более 7.

[Евгений Машеров]

Разумеется, для содержательных советов стоило бы изучить предметную область, но в порядке вбрасывания идей:
0. (поскольку уже предлагал). Перейти к мультипликативно-степенной модели.
1. Перепараметризовать модель. Скажем, вместо "жиров, белков и углеводов" оставить общую калорийность и белки. Но, может, ввести отдельный учёт по незаменимым аминокислотам.
2. Проверять ну хоть "скользящим экзаменом" (отбрасываем одно наблюдение, строим модель на оставшихся, находим ошибку по этому отброшенному; так повторяем для каждого наблюдения, отбрасывая одно и строя по $n-1$ наблюдению).
3. Использовать критерии, учитывающие число параметров (adjusted-R или F-отношение), чтобы не купиться на видимое повышение точности.

[Andrey_Kireew]

Справедливости ради, учитывая всю тяжесть заболевания и его вероятный исход, важность данной модели, или даже, если хотите "метода", нельзя недооценивать. Ведь она даёт человеку главное - хоть призрачную, но надежду, которая в данной ситуации просто жизненно необходима. Всё остальное уходит на задний план. В данной ситуации человек лишен способности здраво рассуждать. Заостряя внимание на любых, мало мальски подтверждающих свою идею моментах, он склонен "не замечать" факты, способные поставить её под сомнение, а так же избегать любой возможности встречи с этими фактами. В глубине души, он не исключает ошибочности своих представлений, и это внушает ему страх. Страх лишиться последней надежды. Стадия отрицания - это нормально, со временем пройдёт.

[aitap]

Lena-Lisa в сообщении #1446456 писал(а):

Вопрос - как искать другие комбинации параметров

Набор данных, о котором идёт речь - это статья S. H. Holt, J. C. Miller, P. Petocz. An insulin index of foods: the insulin demand generated by 1000-kJ portions of common foods, The American Journal of Clinical Nutrition, Volume 66, Issue 5, November 1997, Pages 1264–1276, откуда Вы пытаетесь найти зависимость между регрессором Glucose AUC ( $\mathrm{mol} \cdot \min / \mathrm{L}$ ) и предикторами Fat, Protein, Sugar, Starch, Fiber, Water ($\mathrm{g}$)?

Я выгрузил набор данных из статьи:

1. X <- structure(c(0.4, 0.3, 0, 0.6, 14.4, 11.9, 13.4, 10.9, 5.4, 9.4, 
2. 5.3, 13.4, 0, 20.1, 16.2, 13, 20, 17.9, 4.6, 1.7, 1, 2.1, 2.6, 
3. 5.4, 0.5, 2.1, 0.8, 1.6, 1, 8.7, 2.1, 2.1, 2.2, 3.1, 6.1, 6.2, 
4. 2.9, 3.2, 4.7, 1.3, 6.9, 6.1, 4.3, 4.3, 2.4, 5.8, 2.9, 11.8, 
5. 5.2, 5.3, 9.6, 2.7, 4.6, 15, 19.6, 19.4, 16.1, 56.3, 8.5, 7.6, 
6. 9.4, 5, 5.2, 7.8, 11.3, 10, 3.9, 8.4, 15.3, 8.7, 9.7, 10.7, 10.9, 
7. 11.7, 56.9, 47.2, 56.5, 50.6, 3.1, 20.1, 8.9, 18.7, 1.3, 36.7, 
8. 37.6, 25.8, 44.6, 1.7, 0.2, 2.1, 0.1, 0.5, 4.2, 16.1, 0, 1.8, 
9. 1.7, 2.4, 0.1, 0.5, 2, 0.7, 3.1, 1.1, 10.2, 14, 31.1, 13.7, 17.1, 
10. 7.5, 13.9, 0, 8.4, 2.2, 0, 18.6, 10.5, 17, 16.2, 40.2, 1.1, 0, 
11. 0, 11.5, 3.7, 22.1, 25.3, 0, 0, 24.9, 23.2, 0, 44.1, 43.7, 37.6, 
12. 56, 52.6, 47.1, 47.8, 45.9, 35.4, 36.1, 27.2, 17, 29.1, 19.8, 
13. 29, 29.4, 3.6, 6.1, 9.1, 12.5, 1.8, 0.7, 1.4, 1, 1.6, 1.7, 0.5, 
14. 0, 0, 2.4, 2.4, 6.2, 0, 0, 11.4, 16.8, 0, 3.3, 6.6, 6.5, 0.4, 
15. 1.4, 3.5, 10.9, 9.2, 3.5, 1.5, 1.4, 2.6, 3.2, 6.6, 4.7, 14.1, 
16. 317, 210.1, 360.9, 539.4, 13.5, 10.7, 16.1, 2.1, 2.2, 3.5, 187, 
17. 74.2, 12.2, 0.6, 1.1, 1.7, 20.9, 119.4, 222, 267.1, 250, 36.1, 
18. 40.3, 41.4, 140, 93.9, 134.8, 132.6, 290.8, 33.8, 110.9, 111.2, 
19. 115, 119.1, 114.1, 333.7, 111), .Dim = c(37L, 6L), .Dimnames = list( 
20.     c("Fruit Grapes", "Fruit Bananas", "Fruit Apples", "Fruit Oranges", 
21.     "Bakery products Croissants", "Bakery products Cake", "Bakery products Doughnuts", 
22.     "Bakery products Cookies", "Bakery products Crackers", "Snacks and confectionery Mars Bar", 
23.     "Snacks and confectionery Yogurt", "Snacks and confectionery Ice cream", 
24.     "Snacks and confectionery Jellybeans", "Snacks and confectionery Peanuts", 
25.     "Snacks and confectionery Potato chips", "Snacks and confectionery Popcorn", 
26.     "Protein-rich foods Cheese", "Protein-rich foods Eggs", "Protein-rich foods Lentils", 
27.     "Protein-rich foods Baked beans", "Protein-rich foods Fish", 
28.     "Carbohydrate-rich foods White bread", "Carbohydrate-rich foods Whole-meal bread", 
29.     "Carbohydrate-rich foods Grain bread", "Carbohydrate-rich foods White rice", 
30.     "Carbohydrate-rich foods Brown rice", "Carbohydrate-rich foods White pasta", 
31.     "Carbohydrate-rich foods Brown pasta", "Carbohydrate-rich foods Potatoes", 
32.     "Carbohydrate-rich foods French fries", "Breakfast cereals Cornflakes", 
33.     "Breakfast cereals Special K", "Breakfast cereals Honeysmacks", 
34.     "Breakfast cereals Sustain", "Breakfast cereals Muesli", 
35.     "Breakfast cereals Porridge", "Breakfast cereals All-Bran" 
36.     ), c("Fat", "Protein", "Sugar", "Starch", "Fiber", "Water" 
37.     ))) 
38.  
39. y <- structure(c(126, 133, 83, 66, 89, 61, 78, 92, 139, 98, 88, 93, 
40. 161, 20, 77, 71, 42, 36, 63, 110, 29, 120, 106, 68, 129, 113, 
41. 50, 74, 148, 70, 110, 106, 91, 93, 65, 80, 59, 12293, 12445, 
42. 8919, 9345, 13097, 14305, 12445, 15223, 14673, 16682, 15611, 
43. 12348, 22860, 3047, 8195, 6537, 5994, 4744, 9268, 20106, 9350, 
44. 12882, 11203, 6659, 8143, 6240, 4456, 4535, 13930, 7643, 8768, 
45. 8038, 9102, 8938, 6034, 5093, 4299, 113, 108, 118, 166, 483, 
46. 178, 113, 200, 331, 218, 167, 172, 133, 214, 169, 109, 268, 135, 
47. 307, 183, 775, 112, 122, 106, 69, 58, 156, 67, 120, 146, 88, 
48. 95, 108, 102, 118, 74, 87, 216, 224, 152, 185, 604, 467, 480, 
49. 436, 354, 441, 415, 479, 407, 564, 367, 239, 64257, 9340, 325, 
50. 504, NA, 281, 247, 166, 145, 117, 91, 93, 284, 209, 189, 195, 
51. 189, 209, 163, 139, 99, 31, 45, 20, 15, 215, 223, 191, 298, 253, 
52. 309, 65, 103, 260, 80, 186, 139, 106, 30, 37, 57, 28, 137, 111, 
53. 62, 40, 42, 22, 21, 38, 82, 52, 47, 53, 53, 34, 13, 25, 74, 79, 
54. 50, 39, 74, 56, 63, 74, 118, 79, 62, 70, 118, 12, 52, 62, 55, 
55. 42, 62, 114, 28, 100, 97, 60, 110, 104, 46, 68, 141, 71, 76, 
56. 70, 60, 66, 43, 60, 40, 82, 81, 59, 60, 79, 82, 74, 92, 87, 122, 
57. 115, 89, 160, 20, 61, 54, 45, 31, 58, 120, 59, 100, 96, 56, 79, 
58. 62, 40, 40, 121, 74, 75, 66, 67, 71, 46, 40, 32), .Dim = c(37L, 
59. 7L), .Dimnames = list(c("Fruit Grapes", "Fruit Bananas", "Fruit Apples", 
60. "Fruit Oranges", "Bakery products Croissants", "Bakery products Cake", 
61. "Bakery products Doughnuts", "Bakery products Cookies", "Bakery products Crackers", 
62. "Snacks and confectionery Mars Bar", "Snacks and confectionery Yogurt", 
63. "Snacks and confectionery Ice cream", "Snacks and confectionery Jellybeans", 
64. "Snacks and confectionery Peanuts", "Snacks and confectionery Potato chips", 
65. "Snacks and confectionery Popcorn", "Protein-rich foods Cheese", 
66. "Protein-rich foods Eggs", "Protein-rich foods Lentils", "Protein-rich foods Baked beans", 
67. "Protein-rich foods Fish", "Carbohydrate-rich foods White bread", 
68. "Carbohydrate-rich foods Whole-meal bread", "Carbohydrate-rich foods Grain bread", 
69. "Carbohydrate-rich foods White rice", "Carbohydrate-rich foods Brown rice", 
70. "Carbohydrate-rich foods White pasta", "Carbohydrate-rich foods Brown pasta", 
71. "Carbohydrate-rich foods Potatoes", "Carbohydrate-rich foods French fries", 
72. "Breakfast cereals Cornflakes", "Breakfast cereals Special K", 
73. "Breakfast cereals Honeysmacks", "Breakfast cereals Sustain", 
74. "Breakfast cereals Muesli", "Breakfast cereals Porridge", "Breakfast cereals All-Bran" 
75. ), c("Glucose AUC, mol • min/L", "Insulin AUC, pmol • min/L", 
76. "Insulin AUC: glucose AUC", "Insulin AUC per g carbohydrate, pmol • min • L-1 • g-1", 
77. "Insulin AUC per g serving weight, pmol • min • L-1 • g-1", 
78. "Glucose score, %", "Insulin score, %"))) 
79.  
80. ySEM <- structure(c(14, 12, 7, 11, 6, 11, 14, 12, 26, 10, 23, 17, 18, 
81. 7, 15, 12, 10, 11, 17, 14, 14, 13, 14, 9, 16, 13, 11, 7, 24, 
82. 11, 11, 14, 10, 8, 12, 9, 9, 1190, 1353, 910, 1074, 2978, 3472, 
83. 2402, 382, 2686, 1896, 1808, 1867, 368, 828, 1577, 679, 1590, 
84. 1017, 2174, 3776, 2055, 1901, 1420, 837, 683, 616, 453, 574, 
85. 1467, 713, 623, 635, 1506, 757, 813, 493, 612, 19, 22, 18, 23, 
86. 244, 54, 21, 57, 104, 65, 33, 38, 27, 88, 78, 32, 153, 92, 103, 
87. 44, 502, 15, 20, 12, 5, 5, 48, 10, 19, 29, 5, 14, 12, 9, 18, 
88. 11, 15, 21, 24, 15, 21, 137, 113, 93, 110, 65, 50, 48, 72, 64, 
89. 153, 71, 25, 15013, 1845, 68, 87, NA, 41, 31, 21, 12, 11, 9, 
90. 12, 30, 19, 13, 15, 31, 18, 22, 13, 14, 3, 5, 2, 2, 49, 54, 37, 
91. 75, 46, 35, 7, 16, 41, 22, 36, 14, 27, 6, 9, 11, 6, 20, 14, 8, 
92. 3, 4, 2, 3, 4, 8, 4, 4, 9, 4, 5, 1, 3, 9, 10, 6, 7, 9, 14, 12, 
93. 11, 24, 13, 15, 19, 18, 4, 9, 16, 18, 16, 22, 18, 13, 0, 17, 
94. 12, 15, 18, 10, 10, 35, 16, 11, 9, 7, 6, 7, 12, 7, 6, 5, 4, 3, 
95. 14, 12, 9, 15, 12, 15, 13, 13, 16, 5, 14, 9, 13, 6, 12, 19, 18, 
96. 0, 12, 6, 12, 11, 5, 5, 11, 12, 8, 5, 6, 6, 5, 4, 4), .Dim = c(37L, 
97. 7L), .Dimnames = list(c("Fruit Grapes", "Fruit Bananas", "Fruit Apples", 
98. "Fruit Oranges", "Bakery products Croissants", "Bakery products Cake", 
99. "Bakery products Doughnuts", "Bakery products Cookies", "Bakery products Crackers", 
100. "Snacks and confectionery Mars Bar", "Snacks and confectionery Yogurt", 
101. "Snacks and confectionery Ice cream", "Snacks and confectionery Jellybeans", 
102. "Snacks and confectionery Peanuts", "Snacks and confectionery Potato chips", 
103. "Snacks and confectionery Popcorn", "Protein-rich foods Cheese", 
104. "Protein-rich foods Eggs", "Protein-rich foods Lentils", "Protein-rich foods Baked beans", 
105. "Protein-rich foods Fish", "Carbohydrate-rich foods White bread", 
106. "Carbohydrate-rich foods Whole-meal bread", "Carbohydrate-rich foods Grain bread", 
107. "Carbohydrate-rich foods White rice", "Carbohydrate-rich foods Brown rice", 
108. "Carbohydrate-rich foods White pasta", "Carbohydrate-rich foods Brown pasta", 
109. "Carbohydrate-rich foods Potatoes", "Carbohydrate-rich foods French fries", 
110. "Breakfast cereals Cornflakes", "Breakfast cereals Special K", 
111. "Breakfast cereals Honeysmacks", "Breakfast cereals Sustain", 
112. "Breakfast cereals Muesli", "Breakfast cereals Porridge", "Breakfast cereals All-Bran" 
113. ), c("Glucose AUC, mol • min/L", "Insulin AUC, pmol • min/L", 
114. "Insulin AUC: glucose AUC", "Insulin AUC per g carbohydrate, pmol • min • L-1 • g-1", 
115. "Insulin AUC per g serving weight, pmol • min • L-1 • g-1", 
116. "Glucose score, %", "Insulin score, %"))) 

И попробовал выполнить похожие действия:

1. # chosen regressor 
2. n <- "Glucose AUC, mol • min/L" 
3.  
4. # the linear model is relatively easy to fit 
5. lin.model <- lm(y[,n] ~ X + 0, weights = ySEM[,n]) 
6. print(summary(lin.model)) 
7.  
8. # nonlinear regression is complicated: 
9. #  - need starting values for all parameters 
10. #  - no guarantees we won't end up in a local optimum 
11.  
12. # for technical reasons we'll have to remove "special characters" from variable names 
13. colnames(X) <- sub(', g', '', colnames(X)) 
14. nonlin.data <- as.data.frame(cbind(X, y = y[,n])) 
15.  
16. # starting values from the linear model (power = 1) 
17. nonlin.start <- list() 
18. nonlin.start[paste0(colnames(X), '_slope')] <- coef(lin.model) 
19. nonlin.start[paste0(colnames(X), '_power')] <- 1 
20.  
21. nonlin.model <- nlsLM( 
22.     formula = as.formula(paste( # some dark magic to build a formula from variable names 
23.         'y ~', paste( 
24.             colnames(X), '_slope * ', colnames(X), ' ^ ', colnames(X), '_power', 
25.             collapse = ' + ', sep = '' 
26.         ) 
27.     )), 
28.     data = nonlin.data, start = nonlin.start, weights = ySEM[,n], 
29.     # some more dark magic to make sure that we don't stop before reaching convergence 
30.     control = nls.lm.control(maxiter = 256, maxfev = 65536) 
31. ) 
32. print(summary(nonlin.model)) 
33.  
34. # print RMSE from both models 
35. print(sqrt(mean((predict(nonlin.model) - y[,n])^2))) 
36. print(sqrt(mean((predict(lin.model) - y[,n])^2))) 
37.  
38. # take one sample out of the model and see how parameters change 
39. lapply(seq_len(nrow(X)), function(i) { 
40.     suppressWarnings(nlsLM( 
41.         formula = as.formula(paste( 
42.             'y ~', paste( 
43.                 colnames(X), '_slope * ', colnames(X), ' ^ ', colnames(X), '_power', 
44.                 collapse = ' + ', sep = '' 
45.             ) 
46.         )), 
47.         data = nonlin.data[-i,], start = nonlin.start, weights = ySEM[-i,n], 
48.         control = nls.lm.control(maxiter = 1024, maxfev = 65536) 
49.     )) 
50. }) -> LOOCV 
51.  
52. # some models still don't converge, skip them 
53. print(summary(t(sapply(Filter(function(x) x[['convInfo']][['isConv']], LOOCV), coef)))) 

Не знаю, какие $ \sqrt{\frac{1}{n}\sum_{i=1}^{n}(\hat{y}_i - y_i)^2} $ даёт предложенная Вами процедура, но у меня на этом наборе данных получается 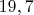$19,7$ для нелинейной регрессии и $22,0$ - для линейной. Вроде бы, это соответсвует найденному Вами улучшению в $10\%$ при переходе к нелинейной модели. К сожалению, найденная при помощи метода Левенберга-Маркуардта формула выглядит как

$$ \mathrm{Glucose} \approx 3 \cdot \mathrm{Fat} ^ {5 \cdot 10^{-6}} + 3 \cdot \mathrm{Protein} ^ {0,1} + 1 \cdot \mathrm{Sugar} ^ 1 + 6 \cdot \mathrm{Starch} ^ {0,8} - 42 \cdot \mathrm{Fiber} ^ {0,1} - 18 \cdot \mathrm{Water} ^ {0,2} $$

А перекрёстная проверка методом вытаскивания даже по одному образцу из обучающего набора (которая, как верно заметил Andrey_Kireew, даёт чересчур оптимистичный результат) показывает разброс для предсказанных значений параметров на порядки, ошибку на обучающем наборе $ \in [ 17,9 ; 20,4 ] $ и на исключённом образце $ \in [ 0,60; 68 ] $. Всё это говорит о переобученности модели; в ней слишком много степеней свободы, и она знает слишком много способов описать набор данных - одинаково хорошо.

[igor_ivanov]

aitap в сообщении #1446607 писал(а):

Я выгрузил набор данных из статьи...

По-моему, Ваши данные содержат пропуски в области "Protein-rich Beef steak". Файл без пропусков здесь.

aitap в сообщении #1446607 писал(а):

$$\mathrm{Glucose} \approx 3 \cdot \mathrm{Fat} ^ {5 \cdot 10^{-6}} + 3 \cdot \mathrm{Protein} ^ {0,1} + 1 \cdot \mathrm{Sugar} ^ 1 + 6 \cdot \mathrm{Starch} ^ {0,8} - 42 \cdot \mathrm{Fiber} ^ {0,1} - 18 \cdot \mathrm{Water} ^ {0,2}$$

Просто на заметку: $\mathrm{Fat}^{5 \cdot 10^{-6}} \approx 1$.

[mserg]

Не исключено, что может сработать система с регуляризацией. В этом случае для достижения повышенной точности можно использовать "неограниченное количество" "регрессоров", что даст необходимую пластичность аппроксимирующей функции. Для борьбы с переобучением нужно использовать регуляризацию. Первое, что приходит в голову, это метод опорных векторов
Программировать ничего не нужно - есть готовые библиотеки. Это одна их самым популярных библиотек регрессии, но сам я ее не пользовался.
Проверка точности все та же - перекрестная.

[Andrey_Kireew]

mserg в сообщении #1446696 писал(а):

Первое, что приходит в голову, это метод опорных векторов

Почему то, мне всегда казалось, что этот метод предназначен для решения задач классификации

[Lena-Lisa]

Andrey_Kireew в сообщении #1446597 писал(а):

Справедливости ради, учитывая всю тяжесть заболевания и его вероятный исход, важность данной модели, или даже, если хотите "метода", нельзя недооценивать. Ведь она даёт человеку главное - хоть призрачную, но надежду, которая в данной ситуации просто жизненно необходима. Всё остальное уходит на задний план. В данной ситуации человек лишен способности здраво рассуждать. Заостряя внимание на любых, мало мальски подтверждающих свою идею моментах, он склонен "не замечать" факты, способные поставить её под сомнение, а так же избегать любой возможности встречи с этими фактами. В глубине души, он не исключает ошибочности своих представлений, и это внушает ему страх. Страх лишиться последней надежды. Стадия отрицания - это нормально, со временем пройдёт.

Восхищена глубиной псих. анализа, старина Фрейд далеко не курит нервно в сторонке, он в самой гуще событий, а его учение вечно живое, даже после того как от него отказались ближайшие соратники.

-- 24.03.2020, 06:54 --

aitap в сообщении #1446607 писал(а):

Набор данных, о котором идёт речь - это статья S. H. Holt, J. C. Miller, P. Petocz. An insulin index of foods: the insulin demand generated by 1000-kJ portions of common foods, The American Journal of Clinical Nutrition, Volume 66, Issue 5, November 1997, Pages 1264–1276
,

Я приводила ссылку и на более раннюю работу, эти ребята плотно взялись в свое время за дело, контролируемо подкармливали студентов в пределах отведенных денег, и изучали реакции, как субъективные(чувство сытости), так и измеряемые - глюкоза, инсулин.

-- 24.03.2020, 07:07 --

aitap в сообщении #1446607 писал(а):

найденная при помощи метода Левенберга-Маркуардта формула выглядит как

$$ \mathrm{Glucose} \approx 3 \cdot \mathrm{Fat} ^ {5 \cdot 10^{-6}} + 3 \cdot \mathrm{Protein} ^ {0,1} + 1 \cdot \mathrm{Sugar} ^ 1 + 6 \cdot \mathrm{Starch} ^ {0,8} - 42 \cdot \mathrm{Fiber} ^ {0,1} - 18 \cdot \mathrm{Water} ^ {0,2} $$

Смущает не укладывающаяся в действительность аппроксимация - практичсески нулевой показатель при жирах (т.е. жиры в таком случае дают постоянный вклад, вне зависимости от своего количества, что абсурдно, при нулевом количестве всего и отклик нулевой); читая дальше, обратила внимание, что это уже замечено форумчанинами - я как акын пою что перед глазами вижу; степень при белках 0,1 - у меня скромнее, всего 0,4 - но факт компрессии и нелинейности подтвержден дважды;
при сахарах и крахмалах ~1 - еще одно подтверждение линейности их влияния, у меня 1 и при жирах, было бы странно если было не так, для организма жиры и углеводы в большой степени взаимозаменяемы, это источники энергии, тактических и стартегических запасов ;
при клетчатке 0,1 - у меня 0,7; низкий показ. степени внушает подозрение, не может 1 г клетчатки действовать почти аналогично 10 г, но тенденция общая, и как и у меня, при клетчатке и воде (у меня не вода, а общий вес, что правильней, автор просто копирует данные исходника, не стараясь вникнуть в суть путем небольшой перекомпоновки) коэффициенты отрицательные - это неопровержимая физиология.
Так у меня нет основания сомневаться в работоспособности полученной мною зависимости - вплоть до получения иных, более обширных и точных данных.

Такие формулы мне встречались и по обработке другой работы Хольт - по сытости (там никаких измерений - опрос и анкетирование) - приведена безумная формула, мне удалось построить более вменяемую. Что интересно - сами авторы даже и не пытались построить зависимомти, ограничились перечнем качественных наблюдений, впрочем самого общего плана - что клетчатка снижает инсулин, белки насыщают и пр. Лишь количественные зависимости позволяют сделать выводы, прогнозы и дать осторожные рекомендации.
Они сделаны - нельзя пить 3 литра воды, как советуют гопники-диетологи, питаться 1 раз, как и 8 раз, нет смысла в раздельном питании - все это отвергалось эволюцией. Хотя инд. особенностей никто не отрицал - но на то врачи, а для прочих здравый смысл и традиции.

-- 24.03.2020, 07:23 --

aitap в сообщении #1446607 писал(а):

у меня на этом наборе данных получается $19,7$ для нелинейной регрессии и $22,0$ - для линейной.

Я после первоначальной обработки данных исключила из набора путем последовательного исключения по одному 8 продуктов, отклонявшихся на 2 сигмы и более - примерно как при обработке экспериментальных данных исключаются выпадающие значения, которые уже невозможно перепроверить. МНК придает слишком большое значения отклоняющимся данным, а такие всегда встречаются - не учтен какой-то компонент пищи, микроэлемент, или кто-то из участников эксперимента в тот день был не в форме и/или у него особое пристрастие к данной еде. Часть продуктов исключалась по глюкозе, часть по инсулину, некоторые выпадали там и там, исключались все. Выпали следующие продукты: вареные бобовые, вареный картофель, кукурузные хлопья с молоком; макароны из муки тонкого помола, йогурт (без сахара), хлеб из непросеянной муки, чечевица, апельсины. Гипотез по поводу одиозности именно этих продуктов не измышляю; но подпали бобовые - они всегда стояли особняком в питании, и не все их способны их благополучно переварить; апельсины богатейший источник витамина С, который не учитывался как предиктор, и пр.
Как Вы справедливо заметили, с ними возможно отклонение составит порядка 20, у меня по оставшимся данным порядка 10-11.
В первом посту особо этого факта не упоминала, меня интересовал метод, мало ли когда еще пригодится, интересовало мнение специалистов, а у него даже оказалось название.

P.S. Я искала решение в "найти решение" Экселя, который по данному набору справляется с 7 переменными, но отказывает при 12. Устойчивость решения проверялась путем малого шевеления исходных данных, катастрофы не происходило. А при 12 переменных решение шло в разнос, что я отношу за счет малости наблюдений.

[mserg]

Andrey_Kireew в сообщении #1446704 писал(а):

mserg в сообщении #1446696 писал(а):

Первое, что приходит в голову, это метод опорных векторов

Почему то, мне всегда казалось, что этот метод предназначен для решения задач классификации

Объяснить, почему вам так кажется, я не берусь.

В английской версии регрессия есть. На Kaggle, и не только, точно видел, что пользуются этой регрессией. При классификации используются подмножество граничных точек, тот же прием применяется для регрессии - см. например scikit learn.

Но, не суть. "Стандартные" пакеты той же линейной регрессии содержат нормы регуляризации L1 и L2.

Сама идея в чем. Усложняя функцию, чтобы добиться ее пластичности, быстро приходим к переобучению - слишком много "степеней свободы". Регуляризация дает возможность и иметь функцию с "любым" числом параметров, и ограничить ее пластичность. Таким образом, подбор параметров регуляризации с одновременной перекрестной проверкой позволяет надеяться на увеличение точности.

[B@R5uk]

А можно табличку исходных данных поиграться? Но только в самом простом виде: каждая строка — отдельное наблюдение, первый столбец — зависимая величина, а все остальные столбцы — аргументы зависимой величины.

[mserg]

B@R5uk в сообщении #1446763 писал(а):

А можно табличку исходных данных поиграться?

igor_ivanov в сообщении #1446675 писал(а):

Файл без пропусков здесь
.

[Евгений Машеров]

Ну, показатель степени при жире таков, что после возведения получается единица с погрешностью порядка ошибки вычисления (кроме двух наблюдений, апельсины и jellybeans, для которых задано точно нулевое содержание жира, но после подстановки значений содержания жира, взятых из других источников, получается та же единица плюс-минус стотысячные). То есть данное слагаемое играет роль свободного члена.
Простая линейная модель дала коэффициенты
94.1757327
-2.24639099
-1.00349455
0.754992881
0.745687365
-1.71647755
-0.0331100596
(первый - свободный член, далее Fat Protein Sugar Starch Fiber Water; все незначимые)
Пошаговая регрессия дала
136.716587
-3.67666193
-1.86494752
-2.10876694
(свободный член, Fat Protein Fiber, уровни значимости для коэффициентов при переменных 0.00000376651587 0.00000948694469 0.0288730208)
Анализ графиков зависимости остатков от переменных на необходимость вводить нелинейную зависимость не указал (что, разумеется, может быть и продукт малости выборки).
Ну и попытка сделать модель, включив квадраты и попарные произведения регрессоров (разумеется, только пошаговая регрессия)
b Std.Err. t(32) p-value
Intercept 122.9069 7.002910 17.55083 0.000000
Protein*Fat -0.1456 0.067443 -2.15877 0.038473
Fiber*Fat -0.5054 0.214300 -2.35843 0.024626
Protein*Protein -0.0262 0.007522 -3.48727 0.001441
Fiber*Sugar -0.0576 0.028123 -2.04920 0.048715
Fat -1.7156 1.007769 -1.70240 0.098378
Интерпретировать не возьмусь, но коэффициент корреляции 80.4%