Доказательство Гипотезы Била.
Гипотеза Била — гипотеза в теории чисел, обобщение Большой теоремы Ферма, где, если

(1); и A, B, C, x, y, z Є N, а x,y, z >2, то A, B, C имеют общий простой делитель.
То есть, необходимо доказать, что равенство (1) возможно только при наличии в основаниях общих простых сомножителей.
Составлять необходимые для анализа равенства можно , например,
по следующим формулам:

; (2а)
или

; (2 в)
где:
Q, q – натуральные взаимно простые числа, основания степеней
Q>q;
n – натуральное число, показатель степени. Можно представить n, как произведение сомножителей:

;
Количество сомножителей неограниченно, т.е. и каждое слагаемое и сумму в исследуемом выражении можно представить как степень с различными вариантами показателей. Количество вариантов зависит от количества сомножителей в n и также может быть неограниченным.
Как видно из уравнений 2а и 2в, мы получаем возможность составлять равенство (1) для n, отличающихся на единицу, рассматривая изначально, любые, либо разности, либо суммы степеней
Пример для уравнения 2а:
подставим числовые значения Q,q,n в левую часть равенства:

;
в правую часть:

Как видим, результаты идентичны, т.е. равенство 2а истинно.
Также с другими числами.
Левая часть:

;
Правая часть:

;
Пример для уравнения 2в:
Левая часть:

.
Правая часть

.
Как видно из приведенных примеров, при составлении равенств по формулам 2а и 2в можно использовать различные основания и показатели степеней, как простые, так и составные.
Уже из приведённого примера для равенства 2а видим, что и каждое слагаемое, и сумму можно представить, как степень с 3-мя вариантами показателей.
Итак, можно составлять равенства, с наличием всех возможных показателей степеней, как сомножителей в произведении n.
Как известно, любое равенство можно преобразовать в другое, добавляя или вычитая из левой и правой его частей определённую величину. Зададимся вопросом:
возможно ли любое из полученных равенств, преобразовать в равенство, опровергающее гипотезу Била?
Для составления такого равенства, необходимо подобрать основания степеней таким образом, чтобы по любому модулю обеспечивалось тождество левой и правой частей равенства, и основания степеней не имели бы общих сомножителей.
Это равенство назовём равенством Х.

; Х
Преобразуем равенство 2а, возведя в квадрат левую и правую его часть
(метод дополнительного неизвестного).
![$$[(Q^n-q^n)^n\cdot q^n+(Q^n-q^n)^{(n+1)}]^2= [(Q^n-q^n)^n\cdot Q^n]^2$$ $$[(Q^n-q^n)^n\cdot q^n+(Q^n-q^n)^{(n+1)}]^2= [(Q^n-q^n)^n\cdot Q^n]^2$$](https://dxdy-04.korotkov.co.uk/f/3/9/4/394750ecd5b064d0ecdfafd343eec76d82.png)
; (2а.1)

; (2a.2)
Сократим на

для упрощения формализованных расчётов, получаем:

; (2a.3)
Итак, первое слагаемое и сумму в равенстве (2a.3), всегда можно представить чётной степенью.
Для этого варианта остаётся ответить на вопрос: можно ли представить степенью второе слагаемое:

, которое после преобразования принимает вид:

?
Очевидно, что получение в произведении точной степени посредством и сложения и вычитания степеней в сомножителях невозможно, так как данные сомножители не могут одновременно быть степенями, с одинаковыми показателями степеней.
Для данного варианта гипотеза Била доказана.
Для доказательства случая, когда сомножитель 2 в показателях степеней отсутствует, произведём корректировку первого слагаемого и суммы в равенстве (2a.3), заменяя показатель 2n на n.
При этом, первое слагаемое уменьшилось на величину
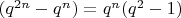
; а сумма на величину

. Для корректировки равенства (2a.3) из второго слагаемого, величины

вычитаем разность корректирующих величин.:

; (2a.4)
После корректировки величины

, получаем:

; 2а.4
Уравнение Била для разности степеней.
Прибегнув к аналогичному рассмотрению равенства 2в, можно убедиться, что и величина

тоже должна быть степенью.
Введя в показатель степени n сомножитель 2 (n=2k) в равенстве 2в, после сокращения получаем возможность анализа на получение точной степени в сумме степеней

.
Для демонстрации проводим аналогичные преобразования равенства

, составленного по аналогии с уравнением 2а,
или

; 2а.5
Преобразуем равенств 2а.5 к равенству

То есть корректируем слагаемые в левой части равенства, а затем и в правой части равенства в сумму;

;
Уравнение Била для суммы степеней.
Таким образом показано, что любое равенство Била может быть преобразовано в предполагаемое равенство Х.
Чтобы получить из степени

степень

методом сокращения необходимо степень

разделить на степень

, а степень

разделить на степень

а их разность

или сумму

, на

или

.
Преобразование таким способом ни для одного возможного варианта уравнения Била обеспечено быть не может,
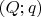
- взаимно простые,
И это справедливо для произвольно выбранных степеней

и

, так как используя равенства 2а и 2в. можно осуществить переход к любому анализируемому варианту.
Чтобы показать, что и показатели степеней с основаниями
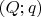
могут быть любыми, рассмотрим пример.
Действительно, например:

; 2a.6
Сократив равенство 2а.6 на


; (2а.7)
и возведя в квадрат правую и левую части равенства 2а.7, получаем:

;

;
Задаём степени для первого слагаемого и суммы:

и

;
Определяем корректирующие величины:

;

;
Корректировка величины приводит к необходимости равенства величины

точной степени.
Аналогичное рассмотрение на основании использования суммы степеней в уравнение Била приводит к необходимости, чтобы и сумма

также была точной степенью.
Что свидетельствует о возможности выражать произвольные степени

через Q и q.
Однако, следует заметить, что возможность преобразования обеспечивается, как и составление исходных уравнений, когда степень у разности
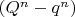
, или суммы

не обозначен, показатель степени равен единице. Но стоит нам обозначить степень разности или суммы, при условии, что показатель степени >2, как становится ясно, что уравнение Била не может быть сконструировано.
Предположим, что разность (Qn- qn) есть точная степень, с показателем f. Величина показателя степени n тоже должyf быть конкретизированf.
Для подтверждения истинности гипотезы Била следует обратиться к оценки равенств посредством использования счисления n.
Как известно, существует строгая закономерность построение разрядов в степенных выражениях.
Построение разрядов в степенных выражениях зависит от принадлежности оснований к конкретным классам вычетов по модулю n, и от рассматриваемой степени.
Понятно, что для того, чтобы уравнение Била, и после сокращения на общие сомножители, и в правой части равенства, и в левой его части, были идентичны, построение разрядов, и после сокращения, идентичность сохраняли. При этом остаётся требование, чтобы построение разрядов соответствовало закономерностям, обусловленными принадлежностью оснований к классу вычетов по показателю предполагаемой степени. Так как о предполагаемой степени, которая предположительно может быть образована, нам ничего не известно, прибегнем к оценки уравнения Била, после сокращения, посредством использования закономерностей, основанных на использовании закономерностей диктуемых показателем степени n.
В качестве примера, рассмотрим вариант, когда Q и q принадлежат к первому классу вычетов по mod n..
Так как при возведении основания, принадлежащее первому классу вычетов по mod n образуется дополнительный младший нулевой разряд, следующий за младшим разрядом, равным единицы, получается, что первое слагаемое в левой части равенства 2а имеет , как минимум, два нулевых разрячда. При этом, второе слагаемое в левой части равенства 2а имеет младших нулевых разряда на один меньше, а в правой части равенства 2а количество нулевых разрядов тождественно количеству младших нулевых разрядов первого слагаемого левой части равенства уравнения 2а, что приводит к невозможности получения целочисленного частного при делении на общий сомножитель.
Принятое конструирование равенства 2а становится невозможным.
Легко убедиться в этом, на основании введения в равенство, напримео 2а, дополнительный сомножитель, принадлежащий к классу вычетов по модулю n, отличных от нуля и единицы.
При умножении равенства 2а на дополнительный сомножитель F, для его сохранения, необходимо умножать на данный сомножитель как Q и q, находящиеся в скобках, так и являющихся сомножителями.
Зададимся принадлежностью к классам вычетов модулю n =3:
Q≡2, по mod n; q≡1, по mod n;
Получаем равенство 2а, выраженное в модулях:
(2n-1n)n×1n+(2n-1n)(n+1)= 2n-1n)n×2n; получаем равенство:1+1=2;
Производим введение дополнительного сомножителя, относящегося ко второму классу вычетов по mod n, результат:
1+2≠2;
Это свидетельствует о том, что уравнение Била, при соблюдении закономерностей, присущих степенным выражениям, не подходит.
То есть уравнение Била, с требуемыми аргументами, обеспечено быть не может.
Это противоречие и свидетельствует о том, что ни разность степеней, ни их сумма, не может быть точной степенью, потому что уравнение Х не возможно, как и опровержение Большой теоремы Ферма. [2]
Что и требовалось доказать.