ЗАДАЧИ студенческой олимпиады им. Н.И.Лобачевского
Казань, 1 декабря 2019 г.
1. Дан многочлен

, где все

,

. Сколько положительных корней может иметь этот многочлен?
2. Доказать, что для любых векторов

и

в пространстве

произведение

не положительно. Когда это произведение равно нулю?
3. Непрерывно дифференцируемая функция

,

, удовлетворяет условию:

для всех

. Найти все вещественные нули функции

.
4. На плоскости даны два эллипса с одинаковыми осями, касающиеся один другого в вершинах:

с уравнением

и

с уравнением

. По каким траекториям будут двигаться фокусы эллипса

при качении этого эллипса вокруг эллипса

?
5. Каждый студент группы из

-ти студентов симпатичен не более, чем двум студентам этой группы. Отношение симпатии, вообще говоря, не является симметричным.
a) Доказать, что в группе найдется

студентов, попарно не симпатичных между собой (3 балла).
б) Какое наибольшее количество произвольным образом выбранных студентов можно отчислить, чтобы по прежнему гарантированно нашлись

попарно не симпатичных студентов? (4 балла)
6. Имеется два тела одинаковой массы и одинаковой теплоемкости. Температура первого тела

, второго

. Можно ли нагреть первое тело за счёт теплообмена со вторым до температуры

, если второе тело произвольным образом можно делить на части? Предполагается, что теплообмена с окружающей средой нет, при соприкосновении двух тел с температурами

и

и массами

и

, их температура мгновенно выравнивается до

.
7. Доказать неравенство:

.
8. Последовательность целых чисел такова, что

,

для всех натуральных

. Каково наименьшее возможное значение выражения

?
9. а) Для матриц

и

размера

проверить, что след матрицы

равен нулю (2 балла).
б) Доказать, что для любой вещественной матрицы

размера

с нулевым следом существуют такие вещественные матрицы

и

, что

(5 баллов).
Примечания. Следом матрицы называется сумма элементов главной диагонали. Операция
![$[B,C]=BC-CB$ $[B,C]=BC-CB$](https://dxdy-02.korotkov.co.uk/f/d/d/7/dd74e91d5c3ede10c768c19cf38729d782.png)
называется коммутатором

и

. Т.о., требуется доказать для матриц

, что след матрицы равен нулю тогда и только тогда, когда матрица является коммутатором. За доказательство существования комплексных матриц

и

в пункте б) -- 4 балла.
10. За круглым столом сидят

(
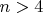
) человек. Все они, независимо друг от друга, случайно (с вероятностью

) выбирают кого-то из своих соседей. Найти: a) среднее количество людей, которых никто не выбрал (2 балла); б) дисперсию этого количества (5 баллов).
Напоминание: если

-- среднее (математические ожидание) случайной величины

, то дисперсия

подсчитывается по формуле

.
11. Николай начертил две равновеликие фигуры: правильный пятиугольник с прямыми углами при вершинах и правильный треугольник. Чему равны углы при вершинах треугольника?