Hint: complex numbers

Complex numbers who?
Basically... Using complex algebra, we just are to find the minimum of complex function
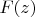
, which real part is
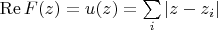
, where
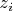
are given.
But laplacian of absolute value is its reciprocal, hence it never equals to zero (except for the points about infinity, and we can't talk about minimum there). Thus, it is impossible to find such a real function
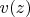
so that

and
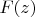
is differentiable at least somewhere.
I don't see if complex algebra made any difference. Worse, maybe - it led to nothing. At least derivation of
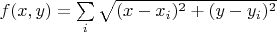
gives equations which are numerically solvable.