Шарик прыгает на движущейся пластинке

[Mathew Rogan]

Помогите разобраться с задачей.

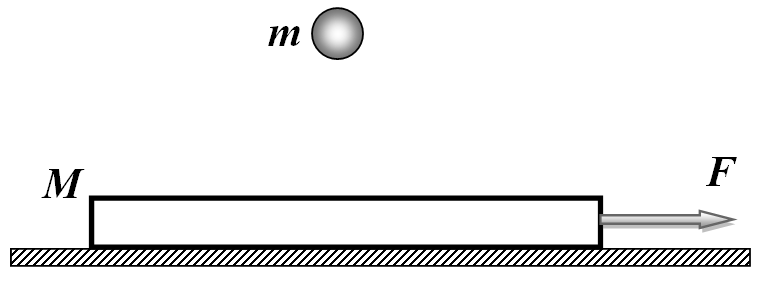
На пластинке массы $M$, движущейся по поверхности шероховатой плоскости под действием силы $F$, вертикально прыгает шарик, упруго ударяясь о пластину. Найти массу шарика $m$, при которой средняя скорость движения пластины постоянна. Коэффициент трения между пластиной и плоскостью $µ$. Время удара шарика о пластину мало.



Как я рассуждаю?

Пусть время между ударами шарика равно $T$. Двигаясь с ускорением $a_1 = \frac{F}{M} - µg$, за время $T$ пластинка увеличивает скорость на $ \Delta\upsilon_1 = (\frac{F}{M} - µg)T$.

Если время удара $t$, то в этот промежуток времени сила трения становится больше и тормозит пластинку. Ускорение теперь равно $a_2 = \frac{F}{M+m} - µg$; за время $t$ пластинка тормозится на $ \Delta\upsilon_2 = (\frac{F}{M+m} - µg)t$.

Чтобы средняя скорость движения оставалась постоянной, должно выполняться $ \Delta\upsilon_1 + \Delta\upsilon_2 = 0$.

Тогда:
$ (\frac{F}{M} - µg)T + (\frac{F}{M+m} - µg)t = 0$.

Но это ничего не даёт. Видимо, надо идти другим путём.

[realeugene]

Задача для устного счёта. Ей место в ПРР.

[Pphantom]

Тема перемещена из форума «Олимпиадные задачи (Ф)» в форум «Помогите решить / разобраться (Ф)»

[realeugene]

Mathew Rogan,
вспомните про закон сохранения импульса.

[Mathew Rogan]

realeugene в сообщении #1425329 писал(а):

Mathew Rogan,
вспомните про закон сохранения импульса.

Я уже понял, что надо идти через него, но что-то не пойму, как его верно применить. Вижу только, что условие малости времени удара дано для того, чтобы пренебречь импульсами сил.

[realeugene]

Mathew Rogan в сообщении #1425345 писал(а):

Вижу только, что условие малости времени удара дано для того, чтобы пренебречь импульсами сил.

Я не знаю, зачем оно дано.

Рассмотрите силы, действующие на нижней стороне пластины.

1. Как связаны мгновенные значения вертикальной силы давления пластины на стол и горизонтальной силы трения?
2. Как связаны импульсы этих сил за некоторый произвольный промежуток времени?

[EUgeneUS]

Mathew Rogan в сообщении #1425296 писал(а):

Если время удара $t$, то в этот промежуток времени сила трения становится больше и тормозит пластинку. Ускорение теперь равно $a_2 = \frac{F}{M+m} - µg$;

Да ладно.
Шарик прыгает, а не ложится на пластину.

[Vladimir-80]

Mathew Rogan в сообщении #1425345 писал(а):

Вижу только, что условие малости времени удара дано для того, чтобы пренебречь импульсами сил.

Скорее наоборот, пренебречь можно увеличением веса пластины в момент удара, а вот импульсы как раз надо считать.

[realeugene]

Ничем тут пренебрегать не нужно Кроме трения между шариком и пластинкой в момент удара.

[pogulyat_vyshel]

Через $V$ обозначим скорость шара в момент удара; через $v_+$ обозначим скорость пластинки сразу после удара ;через $v_-$ -- скорость пластинки за мгновение до удара
Если $Mv_-<\mu N,\quad N=2Vm$ то $v_+=0$ в противном случае $M(v_+-v_-)=-\mu N$

[realeugene]

Кстати, да: для массы шарика можно найти только нижнюю границу. Которая равна нулю, если $F \le \mu M g$

[guryev]

Если считать, что ускорение шарика в процессе удара постоянно, то можно найти его массу как предел при $t/T \to 0$, где $t$ - время удара, $T$ - время между ударами.

[realeugene]

guryev в сообщении #1425586 писал(а):

как предел

Предел чего?

[pogulyat_vyshel]

guryev

ой бросьте, по-существу уже все формулы написаны
если $F-\mu Mg\le\mu mg$ то скорость пластинки является периодической функцией времени и соответственно постоянна в среднем. Иначе скорость пластины в среднем растет

[Утундрий]

pogulyat_vyshel в сообщении #1425588 писал(а):

если $F-\mu Mg\le\mu mg$ то скорость пластинки является периодической функцией

Здесь должен быть знак равенства.