Доброго времени суток! Есть у кого-нибудь соображения насчет проблемы ниже?
Положим, что имеем функцию

, удовлетворяющую условиям:
1. Функция

возрастает, т.е.

, где

- множество положительных чисел

;
2. Функция

- однородная функция первого порядка, т.е.

=


,

;
3. Функция

положительна.
Обозначим через

пространство всех действительных, положительных функций, которые определены на

.
Обозначим через

совокупность всех возрастающих, однородных, положительных функций, определенных на

.
Проблема состоит в следующем: имеет ли место возможность задать такую топологию на

, чтобы множество

являлось замыканием множества

в
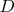
?
Благодарю за содействие!