Влияние космологического расширения на Солнечную систему

[pupugai]

Влияет ли расширение Вселенной на орбиту Земли вокруг Солнца?
В статье The Influence of the Cosmological Expansion on Local Systems авторы решают проблему двух тел с учетом расширения Вселенной. Они используют метрику Фридмана. И получают, что да, влияет (правда, очень мало: по их расчетам, орбита Земли должна измениться за время существования Солнечной системы на $10^{-24}$ долю, то есть на $10^{-13}$ метра, но это не суть).
Но правомерно ли использование тут метрики Фридмана? Метрика Фридмана верна в предположение, что Вселенная гомогена. Но она гомогена только на межгалактических масштабах, поэтому и применять ее можно только на межгалактических масштабах. Так? То есть, если мы хотим решить проблему двух тел, в предположении, что между этими телами есть материя с плотностью равной плотности Вселенной, которая расширяется, то тогда действительно, нам нужно применять метрику Фридмана, и я верю, что мы получим, что радиус орбиты будет чуть-чуть меняться, как подсчитано в статье. Но так как плотность вещества в Солнечной системе совсем не такая, как во Вселенной, и главное это вещество не двигается вместе с хаббловским потоком, то применять уравнения космологии к этой задаче совершенно не имеет смысла, и я не вижу, как расширение Вселенной может хоть как-то повлиять на орбиту Земли. Или я чего-то не понимаю?
Другое дело - космологическая постоянная. Она конечно влияет и на орбиту Земли. Но всё равно, она не заставляет радиус орбиты меняться со временем (просто радиус будет чуть другой, если бы ее не было). Статья, кстати, написана до того, как открыли темную энергию, поэтому там о ней ни слова.

[Geen]

pupugai в сообщении #1418301 писал(а):

Но правомерно ли использование тут метрики Фридмана?

На мой взгляд, и строго говоря - нет. Но для рассмотрения модельного случая, для получения оценки, в качестве первого приближения и очень существенного упрощения - можно. Всё равно, даже ошибка на десяток порядков, не приведёт ни к каким измеримым эффектам.

[Munin]

pupugai в сообщении #1418301 писал(а):

Влияет ли расширение Вселенной на орбиту Земли вокруг Солнца?

Я эту задачу подробно рассмотрел на форуме modcos, а потом скопировал свои объяснения сюда.
Там: http://www.modcos.com/forum/viewtopic.php?f=15&t=57&start=10#p550 , #p557 , #p583
Здесь: post608988.html#p608988

Кроме того:

Munin в сообщении #660986 писал(а):

Задача формально решена здесь: http://www.modcos.com/forum/viewtopic.php?p=355#p355 и здесь: http://arxiv.org/abs/astro-ph/9803097 . Я решения не проверял.

И наконец, начинать надо с Ландау, Лифшица II, § 114, формулы (114.20)-(114.22) в конце параграфа.

TL;DR:

pupugai в сообщении #1418301 писал(а):

Но правомерно ли использование тут метрики Фридмана? Метрика Фридмана верна в предположение, что Вселенная гомогена. Но она гомогена только на межгалактических масштабах, поэтому и применять ее можно только на межгалактических масштабах. Так? То есть, если мы хотим решить проблему двух тел, в предположении, что между этими телами есть материя с плотностью равной плотности Вселенной, которая расширяется, то тогда действительно, нам нужно применять метрику Фридмана, и я верю, что мы получим, что радиус орбиты будет чуть-чуть меняться, как подсчитано в статье. Но так как плотность вещества в Солнечной системе совсем не такая, как во Вселенной, и главное это вещество не двигается вместе с хаббловским потоком, то применять уравнения космологии к этой задаче совершенно не имеет смысла, и я не вижу, как расширение Вселенной может хоть как-то повлиять на орбиту Земли. Или я чего-то не понимаю?

Это верно.

Geen в сообщении #1418320 писал(а):

Но для рассмотрения модельного случая, для получения оценки, в качестве первого приближения и очень существенного упрощения - можно.

Это - нет. (Можно рассматривать физические причины расширения, и в случае, когда они допускают перенос на масштаб Солнечной системы, только их и переносить, а не саму модель Фридмана - целиком она не выживает заведомо.)

pupugai в сообщении #1418301 писал(а):

Другое дело - космологическая постоянная. Она конечно влияет и на орбиту Земли.

Только в том случае, если масштаб неоднородностей DE меньше масштаба Солнечной системы. А на это у нас нет никаких гарантий. (Есть только обоснованное предположение, что если DE обусловлена квантово-вакуумными эффектами, то она должна быть однородна до очень малых квантовых масштабов - например, меньше радиуса протона.)

-- 30.09.2019 15:59:44 --

плюс post513572.html#p513572

-- 30.09.2019 16:18:03 --

Собственно, по физике там самый конец:

Munin в сообщении #608988 писал(а):

Munin на ModCos.com в сообщении #p583 писал(а):

Таким образом, когда мы переходим к рассмотрению малых масштабов, на которых усреднение массы несправедливо, космологическая картина равномерно расширяющегося пространства переходит в картину отдельных (разлетающихся!) массивных тел, и такого пространства-времени внутри и между ними, которое соответствует обычным эффектам гравитации, вызванным их массами.

Вот теперь мы готовы рассмотреть "расширение пространства" на всех масштабах - от надгалактического, до галактик, до отдельных звёзд в галактиках, и наконец, до отдельных атомов на планетах или в межзвёздном газе. В гравитационно связанной системе - галактике или звезде - пространство-время будет "выпуклым", как и во Вселенной, но не "расширяющимся". "Выпуклость" пространства-времени будет обусловлена массой этой системы. <...> размеры такой системы постоянны, а не увеличиваются или уменьшаются вместе со Вселенной, и обусловлены равновесием внутренних сил (включая гравитацию). В системе, связанной негравитационными силами - пространство-время вообще будет "невыпуклым", риччи-плоским, и его воздействие на тела системы будет попросту гравитационным воздействием внешних масс - типа приливного. Например, атом в лаборатории испытывает приливные силы со стороны Земли, и из-за этого слегка сжат и вытянут, как и Луна. Какую величину имеет эта деформация - можно оценить по обычным ньютоновским оценкам. Понятно, что атом из-за этого воздействия тоже ни расширяется, ни сжимается, ни деформируется, а просто остаётся в постоянно деформированном состоянии, в равновесии со своими внутренними силами.

Возвращаясь к самому-самому началу темы, вспомним, что Вселенная заполнена тремя гравитирующими компонентами: тёмной энергией, тёмной материей и обычной материей. Из них последние два ведут себя так, как я излагал, а тёмная энергия - приводит к "выпуклости" обратного знака, то есть на космологических масштабах - к расходящимся, а не сходящимся геодезическим, как меридианы на горлышке кувшина, а не на сфере. Но хотя на космологическом масштабе тёмная энергия преобладает, при переходе к меньшим масштабам она "выключается" первой. Неоднородное распределение тёмной и обычной материи выглядит как шары положительной плотности массы (галактики и скопления в сумме с тёмными гало), погружённые в пространство с отрицательной плотностью массы. Только эта отрицательная плотность - очень мала, и сравнительно может считать нулём. Дальше уменьшая масштаб, мы увидим, что внутри нашего шара положительной плотности выделяются более мелкие объекты положительной плотности - погружённые в пространство с положительной плотностью, но снова очень малой. Это "выключается" тёмная материя, и роль притягивающих масс полностью переходит к обычной материи - таков масштаб звёзд, планет, звёздных скоплений. Урок, который мы можем отсюда извлечь, состоит в том, что "выпуклость" или "невыпуклость" пространства-времени в нашей системе может быть не точно равной нулю, но оставаться, во-первых, пренебрежимо малой, а во-вторых, неизвестной, поскольку мы не знаем детальной структуры тёмной материи и тёмной энергии на таких малых масштабах. И в-третьих, влияние этой "выпуклости" всё равно будет аналогично влиянию ньютоновской гравитации со стороны тёмной материи и тёмной энергии в объёме нашей системы, а не будет каким-то загадочным "влиянием расширения Вселенной". Внешняя Вселенная ни на что не влияет - точнее, находящиеся поблизости массы влияют своими приливными силами, и только.

-- 30.09.2019 16:37:54 --

плюс ещё в начале темы там:

Munin на ModCos.com в сообщении #p321 писал(а):

Вообще, это некорректная постановка задачи. Задание единого параметра $a(t)$ делается в модели Фридмана-Леметра-Робертсона-Уокера в предположении об однородности распределения массы (более общо, источников гравитационного поля) во Вселенной. Но эти источники - сами складываются из атомов, а также из компонент, микроскопическая структура которых нам абсолютно неизвестна (DE и DM).

Для корректного описания следует перейти от невозмущённой модели FLRW к другой модели на масштабах, на которых возмущения плотности массы становятся сравнимы со средней плотностью $\delta\rho/\rho\sim 1.$ В статье Рубаков УФН 178 (3) 301-308 (2008) https://ufn.ru/ru/articles/2008/3/d/ даётся именно этот критерий, и соответствующий масштаб (масштаб нелинейности возмущений плотности) оценивается в среднем в 15 Мпк, а в нашей окрестности - в 2 Мпк, размер Местной Группы галактик. Для иллюстрации, на масштабах атомов $\delta\rho/\rho\sim 10^{29},$ причём именно данную $\delta\rho$ следует учитывать как гравитационную поправку ко взаимодействию ядра и электрона, имеющую порядок $10^{-39}.$ Это чтобы представлять себе, об эффектах какого порядка вообще идёт речь. Я подозреваю, что поправки, связанные со слабым взаимодействием электрона с ядром, и с адронной компонентой электрона и сильным взаимодействием, абсурдно малые, и то будут больше.

Теперь, к какой модели следует перейти. По большому счёту, надо задействовать полностью ОТО в задаче совместного движения массы и гравитационного поля. К счастью, так как плотности и поля очень слабые, можно использовать ньютоновское приближение. Глобальная космологическая метрика FLRW будет задавать граничные условия для такой задачи. Но она не будет фоновой метрикой, поскольку вместо космологических усреднённых будут рассматриваться истинные источники. (Их, конечно, можно раскладывать на слагаемые $\delta\rho$ и $\rho$ сравнимой величины, но смысла в этом немного.) Какие координаты использовать в постановке такой задачи - можно выбирать произвольно, но в случае использования координат, отличных от физических, необходимо соответственно модифицировать уравнения ньютоновской динамики, вводя ковариантные производные вместо частных. Вряд ли это оправдывает усилия, кроме как в виде упражнения. Кроме того, хотя координаты типа $r=R/a(t)$ и остаются допустимыми, они уже теряют смысл сопутствующих координат, и не могут так называться.

Реальный атом, испытывающий внешние силы, описывается стандартным уравнением Шрёдингера со всякими малыми поправками, соответствующими этим силам. Среди таких сил на первых местах будут взаимодействия с соседними атомами, если атом лежит на столе, или летает в баллоне с газом; и взаимодействия с разнообразными электромагнитными излучениями. Перечисляя разнообразные источники поправок, в которые входит практически весь окружающий атом материальный мир, мы доберёмся до гравитационных сил: атом притягивается к Земле, немножко - к Луне и Солнцу, и т. д. Отвлекаясь от продолжающегося ряда поправок другой природы, и сосредоточившись только на гравитационных, мы постепенно перечислим окружающие атом гравитирующие массы на очень большом масштабе. И только тогда, наконец-то, наступит момент, когда по сравнению с этими поправками будет оказывать некоторое влияние и собственная гравитация ядра и электрона. Все предыдущие поправки были, кроме самых первых, линейными по координате, но гравитация ядра и электрона нелинейна, она немного сместит уровни энергии электрона. И всё. Больше ни к чему она не приведёт. И даже перейдя эту поправку, мы будем ещё очень далеко до хаббловской (в расширяющихся координатах, а в физических вопрос будет уже полностью закрыт). Дальше должны быть учтены гравитирующие массы на всё больших и больших масштабах, пока, наконец, не будет достигнут масштаб нелинейности возмущений плотности, приведённый выше. Только тогда (в расширяющихся координатах) будет учтено среднее космологическое $\rho,$ как средняя плотность массы в шаре, центрированном на ядре, и простирающемся до электрона, и гравитация, создаваемая этой средней плотностью в этом шаре (нелинейная по координате поправка). При том, в том же шаре везде, за исключением ядра, будет компенсирующее это слагаемое отрицательное возмущение плотности. Видно, что подобная поправка совершенно не имеет физического смысла, а остаётся всего лишь диковинным способом счёта "прибавили, и сразу отняли".



[Выше, говоря о гравитирующих массах, которые давали поправки к уравнению Шрёдингера, в них входят, разумеется, не только массы обычного вещества, но и объекты тёмной материи и тёмной энергии (если последняя кластеризована на масштабах больше атомного). Если тёмная энергия кластеризована на субатомных масштабах, что предполагается гипотезами вакуума КТП, то она войдёт в среднюю космологическую плотность массы в атоме, но не в компенсирующую отрицательную поправку - и окажется единственным нескомпенсированным слагаемым, хоть и абсурдно малой величины.]


Атом ни в каких координатах не участвует в хаббловском расширении. Уравнение движения электрона с учётом космологического расширения записывать абсурдно, поскольку все поправки следует учитывать по порядку их количественного убывания.




Munin на ModCos.com в сообщении #p323 писал(а):

...если мы считаем Вселенную заполненной веществом настолько однородно, что размеры неоднородностей меньше размеров атома, то что такое в свете этого "атом", как в нём распределены заряды и массы? Ведь стандартными представлениями квантовой механики и физики частиц при таком предположении пользоваться уже нельзя.
<...>
С другой стороны, возвращаясь к реалистичной физике и масштабу 15 Мпк, если человек желает изучить FLRW модель космологии не просто как фитюльку, набор формул, а с пониманием её физического содержания, то он должен понимать, а в преподавании надо акцентировать, что вот эта вот буковка $a(t)$ - есть результат усреднения по большим масштабам от мелких искажений метрики, по сути образованных расходящимся пучком мировых линий галактик (взятых вместе с тёмными гало). Внутри каждой галактики имеется избыток кривизны, а между галактиками пространство-время риччи-плоское (но не полноценно плоское) (пренебрегая на этом уровне DE, которая менее плотна, чем вещество в галактиках). Геометрия такого пространства-времени похожа, если брать низкоразмерные аналогии, на поверхность глобуса, в котором вся кривизна "собрана" в конические вершины с широким углом раскрытия, или в поверхность шатра или мыльной плёнки, "подвешенных" за отдельные точки на растяжках. Для таких поверхностей средняя кривизна в больших масштабах складывается из существенных неоднородностей кривизны в меньших масштабах, и чем меньше масштаб рассмотрения, тем больше эти неоднородности (оставаясь, в то же время, почти всегда далеко в пределах ньютоновского приближения). Вопрос о том, как детально расширяется пространство, необходимо рассматривать именно в таких представлениях, или по крайней мере знать его перевод на этот язык.




Munin на ModCos.com в сообщении #p359 писал(а):

Здесь кроется опасность ошибочной интерпретации, которая, как ни странно, проскальзывает даже в специальной литературе: приписывания космологическому расширению отдельного физического существования, "материальности". В то время как физически надо понимать, что речь идёт исключительно о решении уравнений ОТО с заданными условиями (и помнить их). Это тем более странно в свете получшившей распространение космологической "ньютоновской теории", качественно описывающей эффекты Большого Взрыва, и вместе с тем ясно высвечивающей физический смысл рассматриваемых эффектов и вкладов.


[Напр.:
Нагирнер Д. И. Элементы космологии. - СПб., 2001.]


$a(t)$ не есть функция, заданная сама по себе. ОТО требует совместного решения задачи движения материи и эволюции гравитационного поля, и поэтому $a(t)$ есть решение уравнения Фридмана, обусловленное начальными условиями и средней плотностью материи (и уравнением состояния; а в более полном варианте, набором плотностей и уравнений состояния). В "ньютоновской теории" хорошо подчёркнуто, что сама $a(t)$ обусловлена начальной скоростью разлетающейся материи, и её последующим гравитационным притяжением самой к себе (по закону Ньютона). Ровно то же положение сохраняется и в ОТО: $a(t),$ задающая левую часть уравнения Эйнштейна, и одновременно движение материи по геодезическим, соответствующим постоянным сопутствущим координатам FLRW, обусловлена правой частью уравнения Эйнштейна, то есть гравитационным влиянием материи на пространство и движение материи (видно, что правая часть вся умножена на гравитационную постоянную). Это дифуравнение решается совместно с начальными условиями, аналогичными начальной скорости в "ньютоновской теории".

Итого, истинной физической моделью для рассмотрения атома, планетной системы и т. п., должна быть не "радиальная сила" неизвестной физической природы, а набор конкретных сил известной природы: электрическое взаимодействие с ядром атома и гравитационное взаимодействие с разными источниками. В модели FLRW гравитационные источники (конкретно тёмная энергия, тёмная материя и барионная материя), считается, равномерно распределены в пространстве, но это усреднение больших машстабов, несправедливое в области меньше 2 Мпк. На масштабе 2 Мпк неоднородность барионной и тёмной материи превышает среднюю плотность тёмной энергии - уже здесь нельзя пользоваться производными от $e^{\beta t}.$ Далее, на масштабе примерно 0,3-30 кпк (размеры Галактики) неоднородности барионной материи превышают среднюю локальную плотность тёмной материи. И наконец, ядро атома - неоднородность, значительно превышающая среднюю плотность Галактики. Вместо "радиальной силы" на электрон действует гравитация, о шкалах вкладов которой я уже говорил.

[pupugai]

Спасибо большое за подробный ответ. То есть резюмируя: расширение Вселенной не влияет на Солнечную систему, авторы статьи ошиблись. Правильно?

[Munin]

Чтобы так уверенно сказать, надо бы внимательно с лупой посмотреть на то, какую задачу в какой постановке рассматривают авторы статьи, и что именно они в итоге утверждают.

Но в целом да.

[pupugai]

Я тут подумал, как расширение Вселенной может действительно повлиять на орбиту Земли. Фотоны реликтового излучения заполняют пространство и создают гравитацию. Это значит, что в системе отсчета Солнца на Землю будут действовать все фотоны, которые находятся внутри сферы с центром в Солнце и радиусом 1 а.е. Это эквивалентно тому, что массу Солнца увеличили на энергию фотонов реликтового излучения. Но так как при расширении Вселенной реликтовое излучение испытывает красное смещение, а значит оно теряет энергию, то эффективная масса Солнца будет медленно уменьшаться, а радиус земной орбиты увеличиваться. Правда эффект будет совсем маленький: на несколько порядков меньше, чем подсчитанные в статье $10^{-24}$ а.е. за время существования Солнца.

[Munin]

Разумное рассуждение. Добавьте сюда ещё реликтовые нейтрино ;-)

-- 01.10.2019 18:33:41 --

А ещё эти реликтовые фотоны дают эффект "гравитации Лесажа" между Землёй и Солнцем. Нейтрино, правда, не дают.

Но лесажевские частицы ещё и тормозят Землю на орбите. И эффект Ярковского. Короче, многое надо считать и сравнивать.

[pupugai]

Всё-таки мне сложно принять идею, что в статье ошибка. Поэтому я попытался разобраться. Я нашёл обзорную статью, посвященную этой теме Influence of global cosmological expansion on local dynamics and kinematics. Эта статья в том числе ссылается на статью, с которой началось это обсуждение, но о том, что в ней содержиться ошибка там не говориться. Таким образом приходится признать, что я чего-то не понимаю. Но чего я не понимаю, я пока не понимаю.

Я попытался разобраться, что говорят авторы обзорной статьи. Авторы рассматривают среди прочего влияние космологического расширения (в том числе и без учета космологической постоянной) на Солнечную систему. В частности они рассматривают вопрос о том, может ли космологическое расширение объяснить аномалию Пионеров. Хоть авторы и приходят к ответу "не может", что соответствует моей интуиции, но причина, почему это не было сразу очевидно, и их оценки эффекта мне непонятны.

Ниже мои попытки с этим разобраться.

1. Вначале авторы рассматривают "Newtonian approach" (III.A), где они говорят:

Цитата:

Now note that, in the sense of General Relativity, a body that is comoving with the cosmological expansion is moving on an inertial trajectory, i.e. it is force free.

Это ключевой момент, который мне непонятен. "Cosmological expansion" получается из уравнений Фридмана, которые предполагают, что Вселенная однородна. Но внутри Солнечной системы материя неоднородна и не расширяется (то что Солнечная система не расширяется с хаббловским потоком это несомнено и вопросов не вызывает).

Далее, исходя из этого замечания, авторы добавляют ускорение $(\ddot a /a) R$ (формула (9)) в закон Ньютона и после этого для задачи двух тел получают уравнение (в координатах Ферми):

$$\ddot R = \frac{L^2}{R^3} - \frac {C} {R^2} + \frac {\ddot a}{a} R \eqno(12) $$

То есть они получают то же уравнение, которое использовали авторы статьи, с которой началась эта тема. Иными словами расширение Вселенной (а точнее вторая производная $\ddot a$), по их словам, всё же влияет на Солнечную систему. Я бы понял это, если бы ускорение расширения $\ddot a$ было бы вызвано только темной энергией, но авторы явно говорят, что это верно и для "matter-dominated universe".

2. Далее авторы рассматривают точные решения уравнения Эйнштейна для неоднородной (но сферически симметричной) вселенной. Вначале они рассматривают "matched solution" Эйнштейна-Штрауса (II.B.1). Это решение говорит, что если мы возьмем однородную вселенную с плотностью $\rho$ и сожмем всю материю внутри сферы некоторого радиуса $R$ в центр (то есть вместо $\rho$ поместим в центр тело массы $M=4\pi/3 R^3 \rho$, то решение будет в точности совпадать с решением Шварцшильда внутри сферы, и со вселенной Фридмана снаружи.

Это как раз в точности соответствует моей интуиции: это значит, что расширяющаяся вселенная не будет влиять на то, что происходит внутри. Авторы так же приводят простой аргумент, почему это так: это следует из теоремы Биркгофа (которая является релятивистским вариантом теоремы Ньютона о гравитации сферически симмтеричного тела). Тут всё понятно. Но как это соответствует тому, что они называют "Newtonian approach"?

Кстати, авторы замечают, что решение Эйнштейна-Штрауса работает для matter-dominated universe, что соответствует тому, что мы обсуждали раньше: радиация, хоть чуть-чуть, но может влиять на орбиту Земли.

3. Но потом авторы описывают проблемы, которые возникают с подходом Эйнштейна-Штрауса (в конце секции II.B.1) и рассматривают другое решение. А именно модель МакВитте (V.D). Согласно этому решению движение пробной частицы получается такое же, как в уравнении (12), которое было получено при ньютоновском подходе. Тут я совсем потерял нить: какие физические предположения лежат в модели МакВитте? и как вообще может получиться, что решение Эйнштейна-Штрауса и МакВитте дают совершенно разные ответы? Я конечно понимаю, что решение Эйнштейна-Штрауса неточное для реальной Вселенной, но точное решение должно давать примерно тот же самый ответ, хотя бы в идеальном случае. А тут получаются абсолютно разные ответы!

Авторы говорят, что уравнения Эйнштейна не линейны, поэтому нельзя просто суммировать разные решения. Это конечно так, но всё же какая-то интуиция должна быть, которая объясняла бы, что происходит?

[Munin]

Как-то странно вы читаете, сначала раздел III, потом раздел II. Кажется, надо сначала проштудировать II, и в свете него воспринимать остальное.

Пока смотрю присланную вами статью. Спасибо за неё!

pupugai в сообщении #1419031 писал(а):

Авторы говорят, что уравнения Эйнштейна не линейны, поэтому нельзя просто суммировать разные решения. Это конечно так, но всё же какая-то интуиция должна быть, которая объясняла бы, что происходит?

Доберусь до этого места - посмотрю.

Но мне кажется, этот аргумент неудачен. Уравнения Эйнштейна позволяют хорошую линеаризацию ("линеаризованная ОТО"), которая в свою очередь даёт в пределе теорию Ньютона. Замена ОТО на линеаризованную ОТО неприемлема только в областях сильных полей, и фактически - только в окрестностях чёрных дыр. Так что, мне кажется, интуицию построить как раз вполне возможно, причём многоуровневую:
- Ньютон
- [ ППН = PPN, параметризованное пост-ньютоновское приближение, но я считаю его тут излишним, это скорее для тестов ОТО ]
- линеаризованная ОТО
- полноценная ОТО.

-- 04.10.2019 16:32:02 --

Кажется, авторы в погоне за решениями упускают вопрос о возникновении постановки задачи для этих решений. Мне кажется, его как раз следует не упускать из виду.

А именно, мы не можем заполнять пространство произвольно движущимися или неподвижными, расширяющимися или не расширяющимися компонентами. Мы должны их как-то оправдать (пусть и "на пальцах") исходя из того или иного сценария возникновения той картины, которая наличествует на текущий момент. И в такой ситуации, как мне кажется, автоматически отметаются варианты, в которых (стр. 5)

Цитата:

Gautreau (Gautreau, 1984). Here the matter model consists of two components, a perfect fluid with pressure and equation of state $p=p(\varrho)$ outside the star, and the superposition of this with the star's dust-matter inside the star. However, Gautreau also made the assumption that the matter outside the star moves on radially infalling geodesics, which is only consistent if the pressure outside is spatially constant.

По сравнению с этим, предпочтительней выглядит именно модель Einstein-Straus (Эйнштейна-Штрауса), а именно:
- вещество в центральной неоднородности откуда-то взялось, и скорее всего, собралось из окружающего пространства, из-за чего возник "пузырь" (vacuole);
- вещество в центральной неоднородности претерпело какую-то (оставленную за рамками рассмотрения) динамическую эволюцию, и имеет нулевую начальную скорость (или почти нулевую, но эта скорость не привязана к хаббловскому потоку);
- вещество в "пузыре" (vacuole) не могло остаться безучастным к этому процессу, и тоже не должно по умолчанию считаться участвующим в общем хаббловском потоке. Плотность вещества в "пузыре" (снаружи от центрального тела) не равна средней плотности во Вселенной, а должна быть ниже (в модели Эйнштейна-Штрауса строго 0). Только усреднение по всему "пузырю" даёт плотность, равную средней во Вселенной.

Имхо, нарушая эти соображения, можно наделать много моделей, не имеющих отношения к реальности.

[Munin]

Как я понял линию статьи Giulini (Джулини): автор упоминает Эйнштейна-Штрауса, но потом прочно переключается на модели, в которых "космологическая жидкость" заполняет всё пространство вокруг центрального тела.

Статья обзорная, и в таком случае нельзя винить в этом автора. Он излагает сложившееся состояние в области. Тогда это просто печально. Возможно, нужны публикации, в которых этот аспект разъясняется или хотя бы поднимается для дискуссии.

-- 04.10.2019 17:24:24 --

pupugai в сообщении #1419031 писал(а):

Тут я совсем потерял нить: какие физические предположения лежат в модели МакВитте?

Вот цитата со стр. 6:

Цитата:

McVittie model. This contains a distinguished central object in the sense that the mass within a sphere centered at the inhomogeneity splits into a piece that comes from the continuously distributed cosmological fluid (with pressure) and a constant piece that does not depend on the radius of the enclosing sphere; see our Eq. (82). Moreover, the latter piece is also constant in time, meaning that the strength of the central inhomogeneity remains constant.

[pupugai]

На 18 странице они говорят:

Цитата:

an equation of state, like $p = p(\rho)$, is not assumed

Что это значит с физической точки зрения?
Я понимаю, что в космологии считается, что $p =w\rho$, где w разное для материи, радиации, темной энергии. Но если мы выбрасываем это уравнение, то почему мы можем верить тому, что получится?

[Munin]

Даже интересней: это уравнение состояния - одно из необходимых входных условий для решения уравнения Эйнштейна. Если его не принимать, то метрику можно нарисовать вообще почти какую угодно. (Просто кисточкой рисуем поток сохраняющегося ТЭИ, и подставляем в правую часть.) Иду читать.

[Munin]

pupugai в сообщении #1419290 писал(а):

Что это значит с физической точки зрения?

Вообще довольно странно написано. Уравнения

Цитата:

$$\boldsymbol{T}=\varrho\underline{\boldsymbol{u}}\otimes\underline{\boldsymbol{u}}+p(\underline{\boldsymbol{u}}\otimes\underline{\boldsymbol{u}}-\boldsymbol{g})\eqno(70)$$

$$\boldsymbol{u}=\boldsymbol{e}_0\eqno(71)$$

$$\boldsymbol{e}_\mu:=\|\boldsymbol{\partial}/\boldsymbol{\partial}x^\mu\|^{-1}\boldsymbol{\partial}/\boldsymbol{\partial}x^\mu\eqno(69)$$

означают, что задана какая-то жидкость, текущая по линиям градиента координаты $x^0.$ Ну допустим, поскольку метрика у нас уже задана:

Цитата:

$$g=\biggl(\dfrac{1-m(t)/2r}{1+m(t)/2r}\biggr)^2\boldsymbol{d}t^2-\biggl(1+\dfrac{m(t)}{2r}\biggr)^4a^2(t)\,(\boldsymbol{d}r^2+r^2\boldsymbol{g}_{{\scriptscriptstyle S}^2})\eqno(68)$$

то и "решение" как бы уже есть, и смысл символам $x^\mu$ уже при́дан. Но тогда что, собственно, надо найти? По сути, надо обеспечить сохранение ТЭИ. Видимо, именно это условие и будет заменять собой выкинутое уравнение состояния $p=p(\varrho).$

То есть, делают ещё грубее, чем я написал. Не рисуют кисточкой правую часть уравнения Эйнштейна, а рисуют кисточкой левую часть уравнения Эйнштейна. А потом по ней вычисляют правую. Ну-ну. Поглядим, к чему это приводит.

-- 05.10.2019 21:43:46 --

Жидкость - не жидкость, а "жидкость". Её там называют "жидкостью", но жидкость она только в кавычках. Потому что у реальной жидкости есть уравнение состояния (обычно $\rho=\mathrm{const},\forall\,p$). А тут от жидкости взяли только то, что её ТЭИ пространственно-изотропен в сопутствующей локальной системе отсчёта.

-- 05.10.2019 22:04:07 --

Кажется, я сообразил.

Очевидно, метрика (68) обращается в Шварцшильда при $m(t)=\mathrm{const}.$ А это чёрная дыра. Неестественно для звезды или галактики. То есть, когда мы описываем звезду (из, например, идеальной жидкости), мы вне звезды полагаем метрику Шварцшильдом, а внутри звезды - задаём что-то другое (например, МТУ глава 23).

Значит, это самое решение McVittie (МакВитти) подразумевает, что оно неполно: в центре должен быть какой-то центральный объект, а вокруг него - это самое решение (которое в случае Шварцшильда было вакуумом). Вот оно-то и заполнено этой самой "жидкостью в кавычках", - это "пузырь" (vacuole) между центральным телом и внешней Вселенной, которая FRLW, и с которой надо сшиваться.

Вот в этом физический смысл и есть: смотрят, чем этот "пузырь" может быть заполнен, и как.

-- 05.10.2019 22:06:33 --

Но при этом исходят из того, что он чем-то должен быть заполнен, какой-то "космологической жидкостью", что по-моему, нефизично.

(Реально, конечно, какая-то DM и DE там может быть, но они не жидкость, и не их надо учитывать, и вообще не так уж актуальна задача напрямую сшить дальнюю зону с ближней зоной, между ними большая промежуточная зона...)

-- 05.10.2019 22:12:33 --

pupugai в сообщении #1419031 писал(а):

Тут я совсем потерял нить: какие физические предположения лежат в модели МакВитте? и как вообще может получиться, что решение Эйнштейна-Штрауса и МакВитте дают совершенно разные ответы? Я конечно понимаю, что решение Эйнштейна-Штрауса неточное для реальной Вселенной, но точное решение должно давать примерно тот же самый ответ, хотя бы в идеальном случае. А тут получаются абсолютно разные ответы!

Как я понял по концу стр. 18 - началу стр. 19, решение McVittie получается очень широко параметризуемым. И среди его вариантов есть и Эйнштейн-Штраус, и чего-то ещё.

Где вы нашли "совершенно разные ответы", конкретно для решения McVittie? Я не дочитал, и там много, похоже.

[Munin]

Примерно схожие вещи я излагал в другой теме, решил тоже собрать вместе несколько постов. (Надеюсь, это не помешает вам.)

Munin в сообщении #1385969 писал(а):

Космология в целом на сегодня, грубо говоря, выглядит примерно так:






При этом, сложность верхнего квадратика "базовая модель" намного меньше сложности нижних квадратиков. Основная работа идёт в них. Верхний квадратик практически не меняется (например, не изменился с 1998 года). Но именно он вводит систему понятий, к которой привязываются все остальные.

To be continued...



Munin в сообщении #1385979 писал(а):

Базовая модель описывает Вселенную на двух уровнях, условно говоря, кинематика и динамика.

Кинематика - это какую 4-мерную форму имеет пространство-время Вселенной; как в ней расположены и как движутся различные объекты - галактики, фотоны, пробные частицы; как связаны их характеристики (например, красное смещение фотона) с тем, где они начали и где они закончили движение; каковы астрономические наблюдаемые величины. Сюда же можно отнести горизонты.



Именно кинематике посвящены статьи и лекции С. Попова. Грубо говоря, кинематика - "это то, что должен знать о космологии астроном".


Динамика - это объяснение причин того, что Вселенная такова, какова она есть (описанная в кинематике). За основу берётся уравнение динамики - для искривлённого пространства-времени, заполненного веществом, это уравнение Эйнштейна ОТО. В это уравнение, как исходные данные, подставляются параметры "содержимого" Вселенной, и начальные условия; и вычисляется та самая 4-мерная форма пространства-времени Вселенной, которая известна кинематике. Из неё кинематика уже вычисляет всё остальное. Уравнение Эйнштейна записывается с некоторыми упрощениями, и поэтому выглядит проще, и называется уравнением Фридмана:


$$\dfrac{\ddot{a}}{a}=-\dfrac{4\pi G}{3}\left(\rho+\frac{3p}{c^2}\right).$$

(Технически говоря, там два уравнения, второе из которых даёт эволюцию плотности $\dot{\rho}.$ Здесь выписано уравнение для эволюции масштабного фактора $\ddot{a}.$ Кроме того, само уравнение бывает записано по-разному, и название "уравнение Фридмана" может относиться к разным уравнениям и формам записи.)

Сочетание различных динамических условий даёт большое разнообразие решений уравнений - то есть, "зоопарк" космологических моделей Вселенных.

Главное, на что здесь надо обратить внимание - на причинно-следственные связи. Причинами выступают:


- различные составляющие "содержимого" Вселенной, со своими соответствующими плотностями:

- обычное ("холодное") вещество, в том числе газ, видимые галактики;
- "горячее" вещество, то есть такое, что его частицы движутся с околосветовыми скоростями, и масса мала по сравнению с кинетической энергией; это фотоны реликтового излучения, реликтовые нейтрино, а в ранние горячие эпохи - таким было всё обычное вещество; сегодня доля "горячего" вещества пренебрежимо мала;
- "тёмное вещество", не наблюдаемое иначе как по своим гравитационным проявлениям;
- "тёмная энергия в виде лямбда-члена";
- могут быть добавлены ещё какие-то составляющие.
- уравнения состояния этих составляющих, то есть законы, которым подчиняются энергия, давление, плотность, когда эта сущность сжимается или растягивается, нагревается или охлаждается:

- уравнение состояния "холодного" вещества приписывается обычному и тёмному веществу; ранее была версия, что тёмное вещество "горячее", но она отпала, именно поэтому сегодняшняя модель CDM - Cold Dark Matter;
- уравнение состояния "горячего" вещества;
- уравнение состояния лямбда-члена;
- если есть ещё какие-то составляющие, то для них вводятся другие уравнения состояния.
- начальное состояние движения всех составляющих - принимается за однородное, поскольку расчёт флуктуаций вынесен в отдельную задачу. Это разлёт с большой начальной скоростью. Чем он обусловлен - здесь не рассматривается, хотя этим вопросом занимается отдельная теория инфляции.

Очень важно, что начальное движение не сводится только к движению "содержимого", а также описывает и начальное движение пространства-времени - то есть, расширение Вселенной с некоторой начальной скоростью. Не постулировать этого нельзя - иначе для дифференциальных уравнений не хватит начальных данных. Если попытаться "взорвать" Вселенную в неподвижном пространстве-времени, то получится совсем другое решение - неоднородное и не отвечающее наблюдениям.


Дальше, "содержимое" Вселенной действует гравитацией на всё и вся - на остальное "содержимое". И вследствие этого меняется скорость движения как "содержимого", так и самого пространства-времени.


(Действие гравитации на точечный объект в какой-то момент времени можно представить себе как какую-то силу. Но если речь не о точках или о длительной траектории в пространстве-времени, это представление уже не работает.)


Подчеркну, что само расширение Вселенной везде выступает только как следствие, но нигде не как причина каких-то динамических процессов: разгона, торможения, потери энергии фотоном, и так далее. Причины надо искать среди различных положений и скоростей в неплоском пространстве-времени Вселенной, и различных гравитационных воздействий.

To be continued...



Munin в сообщении #1385992 писал(а):

Теперь про "зоопарк" космологических моделей - множество решений уравнений динамики.


(Упростим себе задачу: пусть Вселенная заполнена только "холодным" веществом и лямбда-членом. От того, что вещество было бы "горячее", частично или полностью, качественно бы ничего не изменилось.)


Базовое понимание причинно-следственных связей хорошо установить, заменив уравнения динамики ОТО на хорошо знакомые и понятные уравнения Ньютона. (Здесь придётся "вынести за скобки" проблемы уравнений Ньютона с бесконечностями, которые ОТО успешно решает.) Этот приём нашёл Милн в 1934 году, и он изложен в


Зельдович, Новиков. Строение и эволюция Вселенной.
Нагирнер. Элементы космологии. (методичка)

Считаем Вселенную однородно заполненной веществом (это важно! это будет сохраняться во всех моделях), и зафиксируем систему координат в нуле, привязав к одной частице. Рассмотрим движение другой частицы. Можно считать, что эта другая частица находится на поверхности сферы радиуса $R.$ Тогда на неё действует сила со стороны массы, содержащейся в шаре, и не действует сила со стороны всей остальной массы Вселенной (так как по Ньютону, внутри массивной сферы сила тяготения ноль; строго говоря, здесь "срезан угол"). Частица движется только радиально, так что


$$m\ddot{R}=-G\dfrac{mM}{R^2}=-G\dfrac{m}{R^2}\cdot\tfrac{4}{3}\pi R^3\rho\qquad\Rightarrow\qquad\dfrac{\ddot{R}}{R}=-\dfrac{4\pi G\rho}{3}.$$

Это ньютоновский аналог уравнения Фридмана. Однако заметим, что $\rho$ эволюционирует вместе с $R$ (частицы становятся плотнее или реже по тому, как "раздувается" Вселенная), и проще использовать


$$\ddot{R}\,R^2=-GM=\mathrm{const}.$$

Это уравнение совпадает с обычным кеплеровским движением по радиусу, и делится на три случая:


- "эллиптическое" движение - ограниченное - когда $M$ достаточно велика: сначала $R$ растёт, потом уменьшается;
- "параболическое" движение - неограниченное - когда $M$ критическая: $R$ растёт, но со скоростью, асимптотически уменьшающейся до нуля;
- "гиперболическое" движение - неограниченное - когда $M$ недостаточно велика: $R$ растёт неограниченно, но с вечным замедлением;

- можно выделить подслучай $M=0,$ тогда $R$ растёт линейно, и скорость всегда постоянна. Это случай "пустой Вселенной".

Эти три случая соответствуют плотности вещества во Вселенной больше критической, ровно, и меньше критической (и ровно нулевой).

Обратим внимание на причинно-следственные связи.
Почему Вселенная расширяется? Из-за начальной скорости (начальных условий).
Почему скорость расширения замедляется? Из-за взаимного притяжения (гравитации). Заметим, гравитация не сама по себе: притягиваются одни массивные частицы к другим массивным частицам.
Почему уменьшается постоянная Хаббла $H$? По обеим причинам: $H$ уменьшалась бы даже в "пустой незамедляющейся" Вселенной, поскольку для конкретной частицы (галактики) $H=v/D,$ а $D$ со временем растёт.
Почему краснеет фотон? В этой модели можно сказать, что чисто по эффекту Доплера: галактика, испустившая фотон, двигалась в тот момент времени с одной скоростью, а галактика, получившая фотон, движется (уже в другой момент времени) с другой скоростью. Эти скорости (пока мы не рассматриваем фазу сжимающейся Вселенной) всегда дают взаимное удаление. Важно учесть, что здесь берутся две скорости в два разных момента времени, и потому в двух разных точках пространства. Также важно иметь в виду, что это объяснение работает только в этой упрощённой модели, а переходя к ОТО, мы должны перейти к более полному эффекту - космологическому красному смещению.

Влияет ли расширение такой Вселенной на связанные системы? Такие как отдельная галактика, планетная система, атом? Вот это вопрос непростой, и я хотел бы его предложить на самостоятельное решение rockclimber и Dmitriy40, с выкладыванием рассуждений в этой теме. (Позже я изложу своё мнение, или сошлюсь на него.)

To be continued... (много получается...)



Munin в сообщении #1386007 писал(а):

Перейдём к ОТО. Уравнение на основе Ньютона заменяется на уравнение Фридмана. Что меняется ещё?
- С точки зрения физики гравитации, источником гравитации становится не только масса (и энергия), но и давление. Это приводит к тому, что нам важно уравнение состояния вещества: от того, что вещество сопротивляется сжатию давлением, оно начинает создавать большее гравитационное поле. Это ключевой элемент, почему вакуум, обладающий фантастически большим отрицательным давлением, создаёт отталкивающее гравитационное поле.
- С точки зрения геометрии, пространство-время может быть искривлено, и даже иметь необычную топологию. Тут важно понимать, что речь о двух разных геометриях и искривлениях: кривизна пространства-времени в целом (4-мерная), и кривизна чисто пространственного сечения (3-мерная). "Чисто пространственное сечение" проводится по определённым правилам, иначе нарушится однородность одномоментного состояния Вселенной. Кривизна связана с "содержимым" Вселенной. Топология остаётся неизменной во время эволюции Вселенной (вообще в ОТО это не всегда так, но в космологии в базовой модели - так).

Так же, как и раньше, Вселенная однородно заполнена "содержимым", и в каждой точке Вселенной мы следим за движением этого содержимого - именно относительно этого локального стандарта мы можем говорить о движении фотонов, пробных тел, о пекулярных скоростях галактик. "Содержимое" составляется из нескольких смешанных компонент с разными уравнениями состояния, и каждая компонента сжимается или растягивается по своим законам сохранения (или переходит в другую, например, "горячее" вещество может остывать и становиться "холодным").

"Старый зоопарк" космологических моделей - это три модели Фридмана-Леметра (я пропускаю "совсем старый" - решения 20-х годов, впоследствии не пригодившиеся, кроме Де Ситтера). "Содержимое" - это только "холодное" ("пылевидное") вещество с плотностью $\rho,$ без давления вообще. Здесь тоже рассматриваются три случая, подобно ньютоновскому варианту:


- когда $\rho$ выше критической: сначала $a$ растёт, потом уменьшается;
- когда $\rho$ критическая: $a$ растёт, но со скоростью, асимптотически уменьшающейся до нуля;
- когда $\rho$ ниже критической: $a$ растёт неограниченно, но с вечным замедлением;

- можно выделить подслучай $\rho=0,$ тогда $a$ растёт линейно, и скорость всегда постоянна. Это случай "пустой Вселенной" - модель Милна.

Сразу же было замечено, что эти три модели соответствуют трём вариантам пространственной (3-мерной) кривизны, так что:


- когда $\rho$ выше критической: пространственная кривизна положительна, и пространственное сечение похоже на сферу, "замкнутая модель";
- когда $\rho$ критическая: пространственная кривизна 0, и пространственное сечение похоже на плоскость, "плоская модель";
- когда $\rho$ ниже критической: пространственная кривизна отрицательна, и пространственное сечение бесконечно и похоже на седловидную поверхность (или плоскость Лобачевского), "открытая модель";

- можно выделить подслучай $\rho=0,$ тогда пространственная кривизна отрицательна и максимальна, радиус кривизны равен возрасту Вселенной. В этом, и только в этом случае, пространственно-временная кривизна (4-мерная) равна 0. По сути, это - необычно рассмотренное пространство Минковского.

Здесь с причинно-следственными связями туго. Нельзя сказать, что вещество своей плотностью определяет топологию пространства Вселенной. Нельзя сказать, что топология определяет собой плотность вещества. Эти вещи находятся в обязательной математической связи: нельзя задать по отдельности какую-то плотность вещества, и какую-то геометрию пространства. Мы вынуждены их всегда согласовывать. Это похоже на уравнения связи в теории электромагнетизма, когда, например, нельзя задать произвольно заряды и электрические поля: между ними всегда должно выполняться уравнение связи $\operatorname{div}\mathbf{E}=4\pi\rho,$ всегда, в том числе и в начальный момент времени.

Но кроме пространственной кривизны, важно понимать и пространственно-временное устройство таких решений. Тут лучше всего смотреть диаграммы Lineweaver & Davis, воспроизведённые С. Поповым. В координатах "собственное расстояние - собственное время" - световые конусы удалённых галактик "наклоняются", пытаясь "разбегаться" будто бы вместе с веществом. На самом деле, это чисто эффект искажения при построении "карты". Он аналогичен тому, как на обычной географической карте по краям параллели и меридианы "съезжают" в стороны, перестают быть перпендикулярными, становятся чаще или реже. Этот эффект можно исправить, выбрав другую "картографическую проекцию" (другие координаты), но тогда будут внесены другие искажения. Приходится выбирать из нескольких зол, и держать в голове оговорки и поправки.

Пробежимся по причинно-следственным связям:
Почему Вселенная расширяется? Из-за начальной скорости (начальных условий).
Почему скорость расширения замедляется? Из-за взаимного притяжения (гравитации).
Почему уменьшается постоянная Хаббла $H$? По обеим причинам.
Почему краснеет фотон? Вот тут уже нельзя сказать, что "чисто по эффекту Доплера". Фотон пробирается от испустившей к получившей галактике через искривлённое пространство-время. В каждой точке пространства-времени он "слушается" местных световых конусов, которые (на одной из "картографических проекций"!) наклонены. Таким образом, фотон воспринимает не только скорости испустившей и получившей галактик в разных местах в разные моменты времени, но и всю линию своего путешествия. Это и заставляет говорить, что эффект вычисляется как космологическое красное смещение. Однако чудесное совпадение приводит к очень простой формуле:


$$\dfrac{\lambda_1}{\lambda_2}=\dfrac{a_1}{a_2}$$

- красное смещение фотона однозначно задаётся всего лишь соотношением масштабных факторов Вселенной на моменты начала и конца его пути. Кстати, кажется, это же работает и для других волн, в том числе досветовых дебройлевских волн элементарных частиц, если на них не действуют по дороге никакие другие силы.

Ещё раз. Фотон краснеет из-за взаимного движения галактик, и промежуточного (за время пути) расширения Вселенной. Но сами по себе эти величины - кинематические. Они сами по себе имеют свои причины: динамику расширения Вселенной, которая возникает из начальных условий, и из всеобщего тяготения всего со всем - всех "составляющих содержимого" Вселенной. Можно сказать и так, что фотон по дороге "чувствует гравитацию" всех составляющих Вселенной. Лишь бы вы умели обращать эти формулировки в формулы.

To be finished... (запланировано ещё одно сообщение)



Munin в сообщении #1386015 писал(а):

Теперь "новый зоопарк" космологических моделей - отличающийся от "старого зоопарка" добавлением $\Lambda$-члена. Эти модели называются, например, решениями FLRW (Фридмана-Леметра-Робертсона-Уокера), а вообще названия не очень устоялись. Пока у нас был один параметр, да ещё пара удачных совпадений, всё было просто. Теперь же, в двух параметрах, возникает вот такое разнообразие режимов:





(взято из http://at-web.physik.uni-wuppertal.de/~kampert/Cosmology-WS0607.html )


Здесь по горизонтали $\Omega_0$ - это плотность "холодного" вещества, выраженная по отношению к критической (1). По вертикали $\Omega_\Lambda$ - плотность энергии $\Lambda$-члена, выраженная в тех же единицах. И что у нас получается?



Expands forever / Recollapses - это знакомый нам параметр "вечного расширения" или "расширения, сменяющегося сжатием. На диаграмме в этом масштабе не видно, но на самом деле, при $\Omega_\Lambda=0,$ граница между двумя вариантами проходит по значению $\Omega_0=1,$ в соответствии со "старыми" моделями Фридмана-Леметра.
Closed / Open - это другой знакомый нам параметр, строение пространственного (3-мерного) сечения: "замкнутое" или "открытое". Обратите внимание! Теперь этот параметр уже не связан однозначно со старым! Возможны все различные комбинации.
Accelerating / Decelerating - раньше нам было знакомо только одно поведение Вселенной: она замедлялась, поскольку гравитация всё притягивает. Но при большом $\Lambda$-члене возникает сильное отталкивание, и Вселенная может не замедляться, а ускоряться. Именно это она сегодня и делает.
No Big Bang - область значений с настолько большой лямбдой, что при продолжении решения в прошлое, Вселенная не сходится в одной точке за конечное время. Она или сходится к нулю по экспоненте - вечно - или "совершает отскок". Решение носит характер $e^t$ или $\ch t.$


Если бы я захотел перечислять все получившиеся варианты, то должен был бы написать 13-19 пунктов. Так что позвольте этого не делать :-) Приведённая диаграмма позволяет самостоятельно разбираться в свойствах различных сочетаний $\Omega_0$ и $\Omega_\Lambda.$

Но где же наша настоящая и единственная Вселенная на этой диаграмме? Примерно в точке 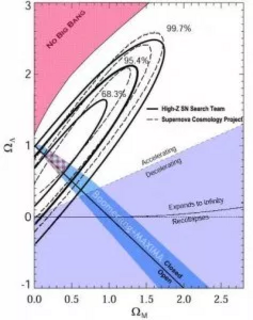$(0{,}3;0{,}7)$





(слайд High-Z Supernova Search Team)


То есть, мы:
- заведомо расширяемся вечно;
- заведомо ускоренно;
- заведомо из Большого Взрыва;
- а вот в "открытой" или "замкнутой" пространственной топологии мы находимся - неясно. Более того, последние измерения (Planck) показывают, что мы балансируем на границе с очень высокой точностью - около 0,1 %.

И снова причинно-следственные связи:
Почему Вселенная расширяется? Из-за начальной скорости (начальных условий).
Почему краснеет фотон? Тут ответ тот же, что и выше.
Почему скорость расширения ускоряется? Из-за отталкивания, превышающегося взаимное притяжение. Опять из-за гравитации! Но теперь "содержимое" Вселенной по большей части состоит из $\Lambda$-члена, а он создаёт гравитацию, отталкивающую всё вокруг. Напомню:


Munin в сообщении #1386007 писал(а):

С точки зрения физики гравитации, источником гравитации становится не только масса (и энергия), но и давление. Это приводит к тому, что нам важно уравнение состояния вещества: от того, что вещество сопротивляется сжатию давлением, оно начинает создавать большее гравитационное поле. Это ключевой элемент, почему вакуум, обладающий фантастически большим отрицательным давлением, создаёт отталкивающее гравитационное поле.


Итак, какие силы действуют на какое-то пробное тело?
1. Силы притяжения со стороны объектов, состоящих из вещества.
2. Силы отталкивания со стороны $\Lambda$-члена того вакуума, который разделяет это пробное тело и окружающие объекты.
И каждый раз можно количественно оценить, какая из них больше, и вообще какую величину они имеют. Силы отталкивания очень слабы на всех привычных нам масштабах: между нами и Землёй, между Землёй и Луной, между Землёй и Солнцем, внутри Галактики, даже между ближайшими галактиками.

И с другой стороны, что действует на пробное тело, кроме сил? Ничего! Действует ли на него расширение Вселенной? Нет! На тело действуют те же условия (силы и начальные условия движения), что и на Вселенную, то есть движение тела и расширение Вселенной - равноправные следствия одних и тех же причин. Равно-уровневые.


Если за этим не следить, то будут ошибки типа "У меня сдуло с головы шляпу, потому что деревья качаются."


На этом пока всё. Если что-то неудачно сформулировал, то уточню.



Munin в сообщении #1386041 писал(а):

Дальше, вопрос хороший: чувствует ли локальная физика масштабный фактор? И если да, то в каком виде?

И ответ, собственно правильный: нет, ни черта не чувствует! Нет у неё никаких механизмов его почувствовать.

Следите за нюансом...
Локальная физика может почувствовать глобальную гравитацию. В ньютоновской модели - глобальный гравитационный потенциал и его градиент (например, нормированный на $\varphi|_{\mathbf{r}=0}=0,\quad\operatorname{grad}\varphi|_{\mathbf{r}=0}=0$). В модели ОТО - глобальную кривизну - радиус пространственной (3-мерной) кривизны. Почему? Потому что вокруг полно источников гравитации, которые вносят свой вклад в эти величины. Их плотность и управляет этими величинами.

Однако для локальной физики источники гравитации неоднородны. Есть Земля, Солнце, Галактика (звёзды и газ), другие галактики. Есть гало тёмного вещества (однородно ли оно? бог знает; но весьма неплотно). Именно эти источники и образуют гравитационный потенциал, который чувствует локальная физика. То есть, какая-то система тел - чувствует гравитацию этих самых тел, и других, окружающих. Если система "погружена" в среду с заметной плотностью (межзвёздный газ, или DM, или DE), то система чувствует и гравитацию этой среды. А если плотность мала - не чувствует.

И только по мере того, как мы рассматриваем бо́льшие и бо́льшие масштабы пространства, все эти локальные источники сливаются в усреднённое однородное "содержимое" Вселенной. И соответственно, создаваемые ими гравитационные потенциалы - в глобальный гравитационный потенциал, который по сути тоже усреднённый.

И в этих абзацах, переходя от ньютоновской модели к ОТО, мы можем заменить "гравитационный потенциал" на "искривление пространства" и его 2-ю производную - на "радиус кривизны пространства (в 3-мерном смысле)".

--------

По мере расширения Вселенной, плотность вещества в ней падает, и тем самым меняется создаваемый этими источниками гравитационный потенциал (в ньютоновской модели), и радиус кривизны (в ОТО). Это локальные величины, и локальные причины и следствия.

А то, что мы можем в формулах выразить их через масштабный фактор - глобальную величину - на физические причины и следствия не влияет.



Munin в сообщении #1386026 писал(а):

Доп. вопрос: какова начальная скорость у Земли вокруг Солнца? У электрона вокруг протона в атоме водорода?

Подсказка: когда взорвалась Вселенная, а когда появилась система Солнце-Земля? И когда появился атом водорода?



Munin в сообщении #1387448 писал(а):

Если мы задаём $a(t)$ "руками", насильно, то получаем неизвестно как взявшуюся историю расширения вселенной. Соответственно, непонятно и что её вызвало. И как это что-то могло повлиять на движения тел и световых импульсов. Поэтому, на самом деле задают не хитрый $a(t),$ а хитрое состояние вещества, а оттуда $a(t)$ получают уже как следствие расчётом. И мы имеем две причинно-следственных связи:
- гравитация вещества с данным уравнением состояния, плюс начальная скорость разлёта вещества, $\Rightarrow$ форма $a(t)$;
- гравитация вещества с данным уравнением состояния, плюс начальная скорость тела (света), $\Rightarrow$ движение тела (света).

[Pphantom]

Выступление Kravchenko Stanislav ликвидировано, пациент забанен как злостный клон.