Теперь поясню, почему меня заинтересовал данный пример.
Рассмотрим последовательность случайных величин
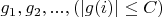
.
Легко показать, что максимум дисперсии случайной величины

достигается, когда случайная величина принимает только значения
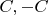
с равной вероятностью.
В этом случае в формуле
![$D[g_i]=M[g_i^2]-M^2[g_i]$ $D[g_i]=M[g_i^2]-M^2[g_i]$](https://dxdy-02.korotkov.co.uk/f/9/0/e/90e1f709e64cd27986a421f9352b604f82.png)
значение
![$M[g_i]=0$ $M[g_i]=0$](https://dxdy-04.korotkov.co.uk/f/f/b/a/fba2e48185957bd17316f2a102ce7bd082.png)
, а
![$M[g_i^2]=C^2$ $M[g_i^2]=C^2$](https://dxdy-02.korotkov.co.uk/f/1/f/b/1fb5bbc8202599a9ca02cd2bf608551e82.png)
, поэтому
![$D[g_i]=C^2$ $D[g_i]=C^2$](https://dxdy-02.korotkov.co.uk/f/1/d/3/1d38920f150b3282ded1c2afe700d73b82.png)
.
Для суммы случайных величин
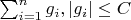
в этом случае также достигается максимум дисперсии, так как в формуле:
![$D[\sum_{i=1}^n {g_i}]=M[(\sum_{i=1}_n {g_i^2})^2]-M^2[\sum_{i=1}^n {g_i}]$ $D[\sum_{i=1}^n {g_i}]=M[(\sum_{i=1}_n {g_i^2})^2]-M^2[\sum_{i=1}^n {g_i}]$](https://dxdy-01.korotkov.co.uk/f/c/9/8/c984f981dad9797158fa50e76e6b7f9b82.png)
значение
![$M[\sum_{i=1}^n {g_i}]=0$ $M[\sum_{i=1}^n {g_i}]=0$](https://dxdy-03.korotkov.co.uk/f/e/c/7/ec7e9d97d4856b20f31fd060524d67de82.png)
,
поэтому
![$D[\sum_{i=1}^n {g_i}]=M[(\sum_{i=1}^n {g_i})^2]=M[(\sum_{i=1}^n {g_i^2)]+\sum\sum_{i \not= j} M[g_ig_j]$ $D[\sum_{i=1}^n {g_i}]=M[(\sum_{i=1}^n {g_i})^2]=M[(\sum_{i=1}^n {g_i^2)]+\sum\sum_{i \not= j} M[g_ig_j]$](https://dxdy-03.korotkov.co.uk/f/e/d/c/edc4079ad84fbbeceb00335375cbd2b982.png)
.
Сделаем оценку первого слагаемого в последнем выражении:
![$|\sum_{i=1}^n {M[g_i^2]} \leq C^2n$ $|\sum_{i=1}^n {M[g_i^2]} \leq C^2n$](https://dxdy-02.korotkov.co.uk/f/5/d/5/5d5067030efb90f58e12242b899006e882.png)
.
В оценке второго слагаемого, используем оценку:
![$|M[g_ig_j]| \leq 1.5C^2/i,i <j$ $|M[g_ig_j]| \leq 1.5C^2/i,i <j$](https://dxdy-01.korotkov.co.uk/f/8/4/3/84386205c9b9809ae24f29e64b1d3d4b82.png)
, поэтому, на основании частичной суммы гармонического ряда, получим:
![$|\sum\sum_{i \not= j} M[g_ig_j]| \leq \sum_{i=1}^{n(n-1)} {1.5C^2/i}=C^2 (3logn+1.5\gamma)$ $|\sum\sum_{i \not= j} M[g_ig_j]| \leq \sum_{i=1}^{n(n-1)} {1.5C^2/i}=C^2 (3logn+1.5\gamma)$](https://dxdy-03.korotkov.co.uk/f/2/e/5/2e5bb88764c11ecd3416635e325eef6182.png)
.
Используя обе полученные оценки получим:
![$|D[\sum_{i=1}^n {g_i}]| \leq C^2 (n+3logn+1.5\gamma)$ $|D[\sum_{i=1}^n {g_i}]| \leq C^2 (n+3logn+1.5\gamma)$](https://dxdy-04.korotkov.co.uk/f/3/9/9/399e05635679472ad9a499d9db90937e82.png)
или
![$D[\sum_{i=1}^n {g_i}]=O(n)$ $D[\sum_{i=1}^n {g_i}]=O(n)$](https://dxdy-04.korotkov.co.uk/f/f/3/8/f38784eaff3434d675278cdab01aaffc82.png)
.
Отсюда следует, что если случайная величина

принимает значения арифметической функции

, т.е. если

, с равной вероятностью и арифметическая функция ограничена -

, то для дисперсии суммы случайных величин выполняется оценка:
![$D[\sum_{i=1}^n {g_i}]=O(n)$ $D[\sum_{i=1}^n {g_i}]=O(n)$](https://dxdy-04.korotkov.co.uk/f/f/3/8/f38784eaff3434d675278cdab01aaffc82.png)
.