Такая задача.
Найти циркуляцию векторного поля
![$F = [xy,xy,z]$ $F = [xy,xy,z]$](https://dxdy-04.korotkov.co.uk/f/f/d/7/fd74e7ba5c91dd8404a96e0677704e5282.png)
по контуру

двумя способами:
1) непосредственно, вычисляя линейный интеграл векторного поля по контуру

2) по теореме Стокса.
Контур задается в первом октанте:
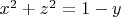
,

,

,

Как понял, это часть часть окружности

и отрезки
![$[0;1]$ $[0;1]$](https://dxdy-03.korotkov.co.uk/f/2/1/a/21ad730ee7df0b97abd700cb0f8426e682.png)
по осям

,

Картинка:
https://yadi.sk/i/DAJi5N__eJ4ziwДалее, как понимаю нужно найти

.
По теореме Стокса:

Так ли? и Как дальше считать?