Да и лучше не на вопросы отвечать (они наводящие), а определить допустимые слова.
Cлово длины

в алфавите

называется допустимым, если
а) Каждая буква входит в слово ровно два раза.
б) Буквы расположены в следующем порядке. Буква

, кроме первой буквы, встречается в слове (при просмотре слева направо) только тогда, когда в слове стоит буква

c
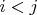
, где

.
-- 03.03.2019, 18:49 --Теперь, пусть дано допустимое слово

. Будем называть буквы

и

в слове
 дружественными
дружественными тогда и только тогда, когда они расположены в таком порядке -
