ins- писал(а):
How did you get it?
Приведу решение для случая, когда т.

лежит в треугольнике

(а Вы докажите для другого случая, ха-ха)
Надо повернуть треугольник

вокруг

, совместив

с

,
и повернуть труеугольник

вокруг

, совместив

с

.
В результате обнаружите на картинке равнобедренный треугольник
с высотой
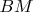
, боковой стороной

и основанием

.