Гипотеза Била

[MMZ]

Формулировка: если $A^x + B^y = C^z $, где $A, B, C, x, y, z $\in$ N$ и $x, y, z > 2$, то $A, B, C$ имеют общий простой делитель.

Доказательство: для доказательства введём понятие коэффициента делимости $D$. Более подробно об этом коэффициенте можно прочитать в работе Л.Ф. Громовой, опубликованной здесь. Нам интересен следующий универсальный признак делимости: число $P$ делится на $T$, если число $P$ без $n$ последних цифр плюс $n$ последних цифр, умноженных на $D^n$ , делится на $T$.

Не теряя общности, можем считать, что $A^x > B^y$, следовательно в системе счисления по основанию $B$ мы можем записать число $A^x$ как $a_1$ - $y$ последних его цифр, $a_0$ - остальные цифры. Тогда:

$$\left\{ \begin{array}{rcl} a_0 + a_1 \cdot D^y = q \cdot A \\ a_0 \cdot 10^y + a_1 = A^x \\ \end{array} \right.$$

Домножим правые части, приравняем их и выразим $a_0$

$a_0 = \dfrac{a_1 \cdot (D^y \cdot A^{x-1} - q)}{10^y \cdot q - A^{x-1}}$

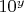
Если $A^{x-1}$ кратно $10^y$, то гипотеза доказана, иначе $a_0 = t \cdot a_1$

Следовательно, $A^x = a_1 \cdot t \cdot 10^y + a_1$

Разделив на $a_1$ и переведя в десятичную систему счисления, получим уравнение

$m \cdot A^{x-1} = B^y \cdot t +1$, которое в натуральных $A, B, t$ имеет единственное решение $m = 1, A = 3, x = 3, B = 2, y = 3, t = 1$, при котором $C^z = 3^3 + 2^3 = 35$ не является степенью натурального числа.

Доказано.

Прошу найти ошибку, не верю, что доказательство может быть столь простым.

[kotenok gav]

MMZ в сообщении #1341242 писал(а):

коэффициента делимости $D$.

Он кажется каким-то странным. Чему он равен, скажем, для 173?

[MMZ]

kotenok gav в сообщении #1341262 писал(а):

MMZ в сообщении #1341242 писал(а):

коэффициента делимости $D$.

Он кажется каким-то странным. Чему он равен, скажем, для 173?

$173 = 17 \cdot 10 +3 $
$D = 17 \cdot 3 + 1 = 52$

[grizzly]

MMZ в сообщении #1341242 писал(а):

не верю что доказательство может быть столь простым.

Приведите, пожалуйста, полное доказательство с учётом этого коэффициента $D$. Беглый просмотр по диагонали показал, что там (у Л.Ф.Громовой) не всегда "Правила делимости" формулируется в виде критериев (необходимости и достаточности) и ничего не говорится о справедливости этих Правил для других систем счисления. Кроме того, там даны правила только для некоторых цифр, на которые заканчиваются числа, а про другие сказано, что не всегда работает. Для каких цифр вы получаете свой результат в системе счисления по основанию $B$?

[kotenok gav]

MMZ в сообщении #1341275 писал(а):

kotenok gav в сообщении #1341262 писал(а):

MMZ в сообщении #1341242 писал(а):

коэффициента делимости $D$.

Он кажется каким-то странным. Чему он равен, скажем, для 173?

$173 = 17 \cdot 10 +3 $
$D = 17 \cdot 3 + 1 = 52$

$170+3\times 52$ не делится на 173.

[mihaild]

MMZ в сообщении #1341242 писал(а):

Число $P$ делится на $T$, если число $P$ без $n$ последних цифр плюс $n$ последних цифр, умноженных на $D^n$ , делится на $T$

На русский это переводится как $\forall T \exists D: \forall n \forall a \forall b < 10^n: (a + b \cdot D^n) \equiv 0 \mod T \rightarrow (a \cdot 10^n + b) \equiv 0 \mod T$, правильно? ($a$ - число без последних цифр, $b$ - последние цифры)
Вроде бы рассматриваются коэффициенты делимости только для модулей, оканчивающихся на $1, 3, 5, 7$ - т.е. взаимно простых с $10$. В таком случае надо взять такое $D$ что $10 D \equiv 1 \mod T$ (ну и получим равносильность)
Для не взаимно простых с $10$ модулей это не работает. Возьмем, например, $T = 4, n = 1$. Имеем $a + bD \equiv 0 \rightarrow 10a + b \equiv 0$. Подстановкой $a = 4$ получаем $bD \equiv 0 \rightarrow b \equiv 0$, откуда $D$ нечетное. Если $D \equiv 3 \mod 4$, то возьмем $a = b = 1$ - посылка выполнена, заключение - нет. Если $D \equiv 1 \mod 4$, то возьмем $a = 1, b = 3$.
В обратную сторону для не взаимно простых с $10$ модулей это тоже не работает - при $b = 0$ истинность заключения зависит от $n$, а истинность посылки - нет.

Итого, определение, видимо, такое: пусть $R$ и $T$ взаимно просты. Тогда коэффициентом делимости для $T$ в системе основания $R$ называется число $D$, обратное $R$ по модулю $T$.

kotenok gav в сообщении #1341309 писал(а):

$170+3\times 52$ не делится на 173.

Насколько я понял, нужно нолик срезать. $17 + 3\times 52$ делится на $173$. Ну и вообще, $10a + b$ и $a + 52b$ делятся или не делятся на $173$ одновременно.

[MMZ]

mihaild в сообщении #1341314 писал(а):

MMZ в сообщении #1341242 писал(а):

Число $P$ делится на $T$, если число $P$ без $n$ последних цифр плюс $n$ последних цифр, умноженных на $D^n$ , делится на $T$

На русский это переводится как $\forall T \exists D: \forall n \forall a \forall b < 10^n: (a + b \cdot D^n) \equiv 0 \mod T \rightarrow (a \cdot 10^n + b) \equiv 0 \mod T$, правильно?

Не знаю, видимо правильно. Я пока ещё не поступил в вуз и в таких символах не силён.

[mihaild]

Тогда получается, что "коэффициент делимости" зависит от того, на что делим, и от основания системы. Для какого модуля и какой системы вы берете $D$?

[kotenok gav]

MMZ
Перевернутая A - "для всех", перевернутая E - "существует", двоеточие - "такое, что".

[MMZ]

mihaild в сообщении #1341314 писал(а):

$10a + b$ и $a + 52b$ делятся или не делятся на $173$ одновременно.

А почему?

-- 25.09.2018, 14:52 --

kotenok gav в сообщении #1341325 писал(а):

MMZ
Перевернутая A - "для всех", перевернутая E - "существует", двоеточие - "такое, что".

Спасибо, буду знать

-- 25.09.2018, 14:55 --

mihaild в сообщении #1341323 писал(а):

Тогда получается, что "коэффициент делимости" зависит от того, на что делим, и от основания системы. Для какого модуля и какой системы вы берете $D$?

Насколько я понимаю, система счисления - всего лишь метод записи чисел. Если $D$ можно вывести в системе с основанием $10$, его можно вывести в системе с любым другим основанием, разве нет?

[yk2ru]

MMZ в сообщении #1341242 писал(а):

можно прочитать в работе Л.Ф. Фёдоровой

Опечатка - фамилия автора Громова.

[mihaild]

MMZ в сообщении #1341336 писал(а):

А почему?

Про это есть отдельная наука, называется "модульная арифметика" (или "арифметика по модулю").
Тут используются такие свойства:
-если $a$ и $b$ взаимно просты, то $c$ и $ac$ делятся или не делятся на $b$ одновременно
-$c$ и $c + bd$ делятся или не делятся на $b$ одновременно.
Попробуйте из этих свойств, и того что $10\cdot 52 = 520 = 173 \cdot 3$ вывести требуемое.

MMZ в сообщении #1341336 писал(а):

Если $D$ можно вывести в системе с основанием $10$, его можно вывести в системе с любым другим основанием, разве нет?

В вашем утверждении участвуют последние цифры числа. А последние цифры зависят от системы счисления.
Если скажем $b < 10$, то $b$ является последней цифрой числа $10a + b$ в десятичной системе. Но не обязательно в какой-то другой.
Например, число $15_{10}$ по основанию $5$ записывается как $30_5$, а по основанию $16$ - как $F_{16}$. Соответственно последняя цифра может быть $5$, может быть $0$, может быть $F$. Ну и естественно после вычеркивания последней цифры мы получаем тоже разные цифры.

[Lia]

Тема перемещена из форума «Дискуссионные темы (М)» в форум «Карантин»
по следующим причинам:

По просьбе ТС для редактирования.

Будьте внимательны: каждая формула должна начинаться со знака доллара и заканчиваться тоже, но в середине формулы их быть не должно. Исправьте.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Lia]

Тема перемещена из форума «Карантин» в форум «Дискуссионные темы (М)»

[yk2ru]

MMZ в сообщении #1341336 писал(а):

Если $D$ можно вывести в системе с основанием $10$, его можно вывести в системе с любым другим основанием, разве нет?

Попробуйте их найти для 16-ой системы счисления. У Громовой похоже нет разъяснений, как получать формулы в зависимости от последней цифры и используемой системы счисления.