Кажется, я улавливаю, о чём речь. Предлагаю следующую формулировку.
Пусть имеется конечное множество

, содержащее

элементов:

. Тогда

Далее мы считаем

эквивалентными, если существует перестановка элементов

, переводящая

в

. Требуется подсчитать число классов эквивалентности(обозначим их множество S) для каждого
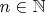
.
Например, для


, S=
Код:
{{{1},{2}},
{{1},{1,2}},
{{1},{2},{1,2}}}.
Для


,S=
Код:
{{{1, 2}, {1, 3}},
{{1}, {2}, {3}},
{{1}, {2}, {1, 3}},
{{1}, {2}, {1, 2, 3}},
{{1}, {1, 2}, {1, 3}},
{{1}, {1, 2}, {2, 3}},
{{1}, {1, 2}, {1, 2, 3}},
{{1, 2}, {1, 3}, {2, 3}},
{{1, 2}, {1, 3}, {1, 2, 3}},
{{1}, {2}, {3}, {1, 2}},
{{1}, {2}, {3}, {1, 2, 3}},
{{1}, {2}, {1, 2}, {1, 3}},
{{1}, {2}, {1, 2}, {1, 2, 3}},
{{1}, {2}, {1, 3}, {2, 3}},
{{1}, {2}, {1, 3}, {1, 2, 3}},
{{1}, {1, 2}, {1, 3}, {2, 3}},
{{1}, {1, 2}, {1, 3}, {1, 2, 3}},
{{1}, {1, 2}, {2, 3}, {1, 2, 3}},
{{1, 2}, {1, 3}, {2, 3}, {1, 2, 3}},
{{1}, {2}, {3}, {1, 2}, {1, 3}},
{{1}, {2}, {3}, {1, 2}, {1, 2, 3}},
{{1}, {2}, {1, 2}, {1, 3}, {2, 3}},
{{1}, {2}, {1, 2}, {1, 3}, {1, 2, 3}},
{{1}, {2}, {1, 3}, {2, 3}, {1, 2, 3}},
{{1}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}},
{{1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}},
{{1}, {2}, {3}, {1, 2}, {1, 3}, {1, 2, 3}},
{{1}, {2}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}},
{{1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}}.
Для вычислений использовался такой код mathematica:
Код:
n = 3; s = Range[n]; Select[
Union[Select[Subsets[Subsets[s]], ! MemberQ[#, {}] &],
SameTest -> (MemberQ[(p = #1;
Map[
Sort, ((p /. # & /@ (Inner[#1 -> #2 &, s, #, List] & /@
Permutations[s]))), 2]), #2] &)], (s1 = #;
s2 = Complement[s, #] & /@ s1;
And @@ (MemberQ[(a = #; If[a != {}, Intersection @@ a, {}]) & /@
Subsets[Union[s1, s2]], {#}] & /@ s)) && (Union @@ # ==
s) &]
Таким образом, при

получается

При


что согласуется с результатами
mustang.