Приведу объяснение для частного случая - уравнения второго порядка - из классического американского учебника авторства Морриса Тененбаума (перевода этой книги на русский, кажется, нет). Объяснение для общего случая есть в большинстве стандартных учебников по ДУ. Очень подробно эта (как и множество других) тема рассматривается в учебнике "Лекции по обыкновенным дифференциальным уравнениям" (авторы Боровских А.В., Перов А.И.). Мне он очень нравится

Если мы рассматриваем случай кратных корней, то изучаемое дифференциальное уравнение второго порядка с постоянными коэффициентами можно привести к следующему виду:

Характеристическое уравнение будет иметь вид

а корнем его будет

(кратности 2).
Пусть

Какой вид должна иметь функция

, чтобы

было решением уравнения (1)?
Если

решение, то должно выполняться
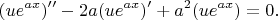
Выполняя дифференцирование, получим

Как видно, выражение в скобках можно упростить. В результате получим

Так как

, то от (2) можно перейти к уравнению

Решение этого дифференциального уравнения:

Таким образом, функция

является решением уравнения (1), если она имеет вид

То, что функции

и
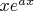
линейно независимы, легко проверить.