Доброго времени суток всем!
Собственно два (как по мне, связанных) вопроса по Зоричу.
1) В пункте о локальном приведении гладкого отображения к каноническому виду есть замечание к теореме о ранге:
Цитата:
Если в любой точке исходной окрестности

ранг отображения
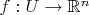
равен

, то точка

, где

, является внутренней точкой множества

, т.е. содержится в

вместе с некоторой своей окрестностью.
Т.е. если ранг отображения меньше

, то точка

может не являться внутренней точкой множества

? (Зорич об этом умалчивает). Тогда она может быть или граничной, или внешней точкой? Тогда какой?
2) Теперь собственно к вопросу о зависимости функций. Дано определение функциональной независимости:
Цитата:
Говорят, что система непрерывных функций

является функционально независимой в окрестности точки

, если для любой непрерывной функции

, определенной в окрестности точки

, соотношение

в окрестности точки

возможно только в случае, когда
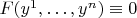
в окрестности точки

.
(Здесь небольшое уточнение: выражение

, как понимаю, следует читать: функция

равна нулю для всех

из окрестности точки

?)
Теперь интересующее утверждение:
Цитата:
Если система

гладких функций, пределенных в окрестности

точки

такова, что ранг матрицы

в любой точке

один и тот же и равен

, то
а) при

система функционально независима в окрестности

;
б) при

найдутся окрестность точки

и такие

функций системы, пусть

, что остальные

функций системы в этой окрестности представляются в виде

где

- гладкие функции, определенные в окрестности точки

и зависящие только от

координат текущей точки

.
При доказательстве пункта а) используется приведенное выше замечание к теореме о ранге. В доказательстве пункта б) ничего существенного нет. После доказательства автор излагает:
Цитата:
Мы показали, что если

, то найдутся

специальных функций

, устанавливающих соотношения

между функциями системы

в окрестности точки

Если исходить из отрицания функциональной независимости, то функционально зависимой будет система непрерывных функций

в окрестности точки

, если найдется непрерывная функция

, определенная в окрестности точки

, для которой будут справедливы соотношения:

в окрестности точки

и

не равна тождественно нулю в окрестности точки

Но если такое утверждение имеет место, то тогда функции

в окрестности точки

, поскольку

, где

- гладкие функции, определенные в окрестности точки

и мы имеем функционально независимую систему. Где я ошибаюсь, подскажите пожалуйста? Это как-то связано с моим первым вопросом? Это собственно и второй вопрос.
Буду благодарен любым подсказкам.