Условие:Решить задачу Дирихле для уравнения Лапласа на прямоугольнике

методом конечных разностей с шагом по осям

и

соответственно

и
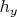
, а

,

,

,
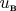
— соответственно значения функции

на левой, правой, нижней и верхней сторонах прямоугольника. Для решения использовать явную трёхслойную схему "крест". Построить диаграмму распределения значений функции

в виде линий уровня.

,

,
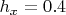
,

,

,
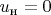
,

.
Что у меня вызывает недоумение: если мы имеем уравнение Лапласа, то, вроде бы, никакой речи про функцию

не может быть, скорее всего имелось ввиду

? Это первое, второе: разве может быть "явная трёхслойная схема "крест"? И третье: не понятно какая температура в углах прямоугольника, насколько я понимаю температура на углах не должна противоречить заданным условиям. Ваши мнения?