Red_HerringНе могу сообразить, почему выполняется равенство (*).

В левой части этого равенства вместо

должно быть

, так?
Получается следующее.
1. Поскольку характеристический многочлен от

имеет степень 4, то

можно записать в виде

т.е. как многочлен степени, вообще говоря, не выше 3, с коэффициентами, являющимися функциями от

.
2. Тогда справедливы равенства

где

- корни характеристического многочлена для матрицы

.
Но откуда следуют эти равенства?
Ведь равенство (*) можно рассматривать как определение функции

:

где

,

- квадратная матрица.
Тогда при

матрица

не определена, так как не существует
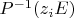
.